基本介紹
- 中文名:對應角
- 外文名:corresponding angle
- 一級學科:數理科學
- 二級學科:數學
- 類型:數學術語
- 套用:全等三角形、相似三角形
全等三角形
對應的來源
簡介
性質
例題


 圖1
圖1




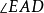

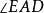
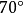
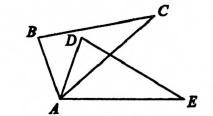 圖2
圖2


 圖1
圖1




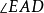

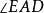
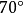
 圖2
圖2當兩個全等圖形完全重合時,相互重合的頂點叫做對應頂點,互相重合的邊叫做對應邊,互相重合的角叫做對應角。實際上,不僅全等三角形有對應邊和對應角,相似三角形中也有...
角邊角公理(ASA):兩個三角形對應的兩角及其夾邊相等,兩個三角形全等。經過翻轉、平移後,能夠完全重合的兩個三角形叫做全等三角形,角邊角公理是證明是兩三角形...
旋轉角是指以圖形在作旋轉運動時,一個點與中心的旋轉連線,與這個點在旋轉後的對應點與旋轉中心的連線這兩條線的夾角。...
(1)平行於三角形一邊的直線和其他兩邊所構成的三角形與原三角形相似;(2)如果兩個三角形對應邊的比相等且夾角相等,這2個三角形也可以說明相似(簡敘為:兩邊對應...
如果兩個邊數相同的多邊形的對應角相等,對應邊成比例,這兩個或多個多邊形叫做相似多邊形,相似多邊形對應邊的比叫做相似比。(或相似係數)...
1. 相似三角形對應角相等,對應邊成比例。2. 相似三角形的一切對應線段(對應高、對應中線、對應角平分線、外接圓半徑、內切圓半徑等)的比等於相似比。...
經過翻轉、平移後,能夠完全重合的兩個三角形叫做全等三角形,而該兩個三角形的三條邊及三個角都對應相等。全等三角形指兩個全等的三角形,它們的三條邊及三個角...
三角函式是基本初等函式之一,是以角度(數學上最常用弧度制,下同)為自變數,角度對應任意角終邊與單位圓交點坐標或其比值為因變數的函式。也可以等價地用與單位圓有...
共角定理(外文名Common angle theorem)內容指的是若兩個三角形有一組角相等或互補,則它們的面積比等於與這一組角相鄰的兩邊乘積的比。別稱鳥頭模型、鳥頭定理。...
位似圖形的任意一對對應點與位似中心在同一直線上,它們到位似中心的距離之比等於相似比。1.位似圖形對應線段的比等於相似比。2.位似圖形的對應角都相等。...
三角函式是基本初等函式之一,是以角度(數學上最常用弧度制,下同)為自變數,角度對應任意角終邊與單位圓交點坐標或其比值為因變數的函式。也可以等價地用與單位圓有...
位似三角形是指兩個每組對應頂點所在的直線都交於一點,對應邊互相平行的相似三角形。...
如果兩個邊數相同的多邊形的對應角都相等,對應邊都成比例,這兩個多邊形叫做相似多邊形。相似多邊形的對應邊的比叫做相似比或相似係數。相似比等於1的相似多邊形就是...
經過平移,對應線段平行(或共線)且相等,對應角相等,對應點所連線的線段平行且相等。平移變換不改變圖形的形狀、大小和方向(平移前後的兩個圖形是全等形)。...
相似三角形對應角相等相似三角形對應高的比、相似三角形對應邊的比、對應中線的比、對應角平分線的比和相似三角形周長的比都等於相似比。當然,其它一些如對應邊所...
