線上性變換中，
由Rn到Rm的一個變換（或稱函式、映射）T是一個規則，把Rn中每個向量x對應以Rm中的一個向量T(x)，Rn稱為T的定義域，而Rm稱為T的余定義域（或取值空間）
基本介紹
- 中文名：余定義域
- 外文名：domain
- 學科：線性代數
符號T：Rn-＞Rm說明T的定義域是Rn而余定義域是Rm，對於Rn中向量x，Rm中向量T(x)稱為x的像，所有像T(x)的集合稱為T的值域.
余定義域
余定義域
相關詞條
- 余定義域
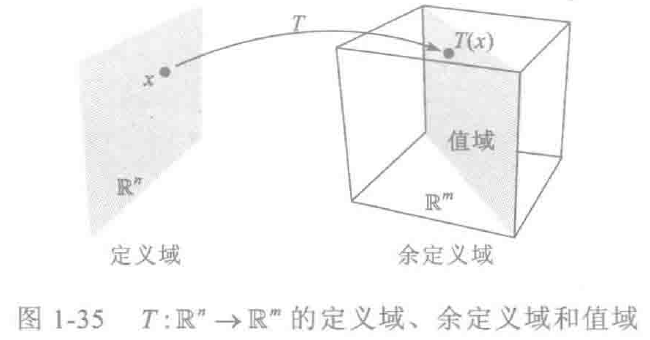
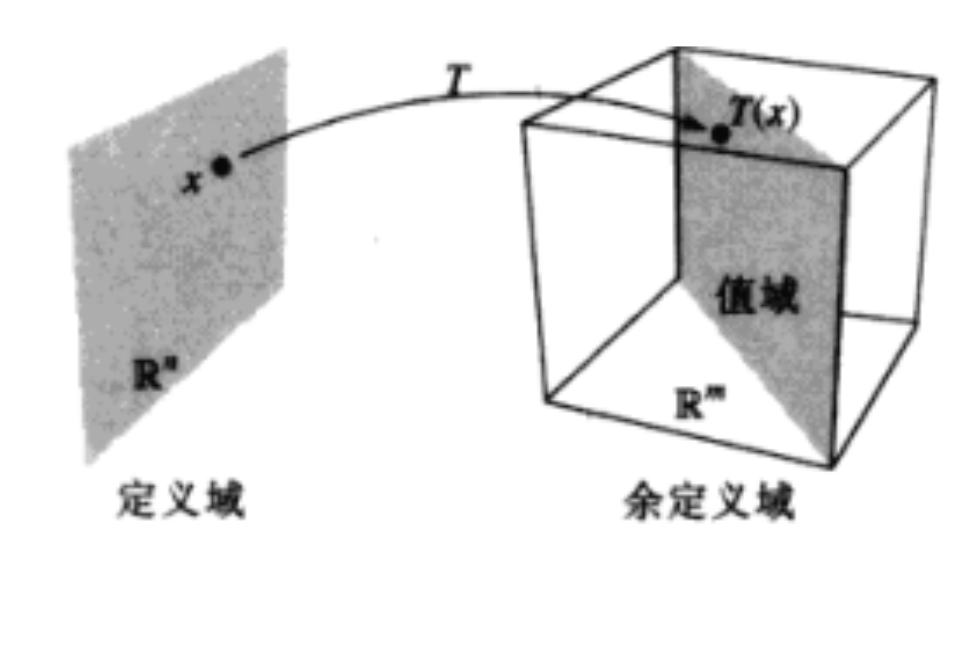
線上性變換中，由Rn到Rm的一個變換（或稱函式、映射）T是一個規則，把Rn中每個向量x對應以Rm中的一個向量T(x)，Rn稱為T的定義域，而Rm稱為T的余定義域（或取值空間）符號T：Rn-＞Rm說明T的定義域是Rn而余定...
- 餘弦(數學概念)
餘弦函式的定義域是整個實數集，值域是 。它是周期函式，其最小正周期為 。在自變數為 （ 為整數）時，該函式有極大值1；在自變數為 時，該函式有極小值-1。餘弦函式是偶函式，其圖像關於y軸對稱。三角形任何一邊的平方等於其他兩邊平方的和減去這兩邊與它們夾角的餘弦的積的兩倍，即在餘弦定理中，令 ...
- 雙曲餘弦函式
雙曲餘弦函式的定義域為 。值域為[1, )。當x=0時，取到最小值1。奇偶性 雙曲餘弦函式在定義域內是偶函式。可以證明。取x的負值。又得：根據加法交換律，可得出 。根據偶函式的定義，可知該函式是偶函式。它關於y軸對稱。單調性 雙曲餘弦函式y=cosh x，在區間 內它是單調減少的，在區間 內它是...
- 余無窮擴張方法
來構造滿足某些性質的集合 A(以U } en}作為c，的定義).與有窮擴張方法不同的是，有窮擴張方法要求這些B，都定義在。的有窮前節上;而余無窮擴張方法則只要求B，的定義域是余無窮集，從而保證每個Bn有足夠的擴張空間.有窮擴張方法是余無窮擴張方法的特殊情況.使用余無窮擴張方法的典型例子是恰對的構造.
- 反餘弦函式
反餘弦函式的定義域為 [-1，1]值域 反餘弦函式的值域 [0，π]單調性 反餘弦函式是單調遞減函式。證明。法一：因為 證畢。於是餘弦函式在該區間上為減函式。所以，由反函式的性質，反餘弦函式為減函式。奇偶性 反餘弦函式是非奇非偶函式。因為反餘弦函式圖像不關於y軸對稱，故不是偶函式；又因為反餘弦函式圖像...
- 高等數學自學及解題指導
片斷：確定函式的定義域，意味著在實數範圍內找出使函式有意義的自變數的取值範圍.正確解題的關鍵在於：（1）搞清五類基本初等函式的定義域，例如偶次方根被開方數應為非負數；對數函式的真數要大於零；反三角正弦、餘弦的定義域是區間[－1，1]等等；（2）明確分式函式的分母不能等於零；（3）熟練掌握解不等式（...
- HSR(路由協定)
組的移動軌跡可以預先定義域，既可以是隨機的移動，也可以是有目的地的移動，每個節點除了組的移動，還有獨立的隨機移動，節點的運動由組的運動矢量GM和隨機矢量RM共同決定，如圖1-2所示。在每個邏輯子網內部，至少存在一個歸屬代理，負責管理所屬節點的當前HID地址（位置管理），並為所屬節點轉發數據分組。為了追蹤...
- 反雙曲函式
雙曲函式y=sinhx的定義是y=sinhx= .那么，取它的反函式，最終得到反雙曲正弦函式的定義是y=arsinhx= 。反雙曲正弦函式的定義域為 。它是奇函式。在區間 內單調增加。反雙曲正弦函式的導數是 。不定積分是 （不包含不定積分特有的常數C）。反雙曲正弦函式的冪級數展開式是： 。反雙曲餘弦 反雙...
- 微積分拾階(1)
表示了依賴關係之後，還必須說明其中自變數的取值範圍。因為在實際問題中，有時候並不能從依賴關係本身就得到自變數的取值範圍。因此還必須單獨規定。這個取值範圍被稱為定義域。有了自變數的取值範圍，加上函式的對應關係，就可以得到因變數的取值範圍，這就是函式的第三個要素，被稱為值域。總結一下，函式概念最關鍵...
- 考點同步解讀:高中數學4
考點1 任意角的三角函式的定義/17 考點2 三角函式的有向線段表示/18 考點3 三角函式值的符號/19 考點4 誘導公式（一）/20 考點5 三角函式式的化簡、求值、證明/21 考點6 三角函式的定義域/Z2 題型·方法 求含有三角函式的複合函式的定義域的兩種題型/2 2 1.2.2 同角三角函式的基本關係 考點1 兩個基本...
- 中學教材全解-學案版高中數學
一任意角的三角函式的定義14 二三角函式的定義域15 三三角函式值在各象限的符號16 四三角函式線16 五誘導公式一17 六利用三角函式的定義求任意角的三角函式值18 七三角函式線的套用18 教材習題答案與解析181 1.2.2同角三角函式的基本關係21 一同角三角函式的基本關係21 二給值求值22 三化簡三角函式式24 四證明...
- 數學題解辭典代數
（1）定義域（1205―1208）（2）圖象（1209―1214）（3）單調性（1215―1220）（4）大小比較（1221―1231）（5）最大值與最小值 閉區間上的最大（小）值（1232―1236）條件極值（1237―1243）其它（1244―1247）（6）雜題（1248―1253）4.指數方程和指數不等式 （1）指數方程（1254―1267）（2）指數方程...
- Project 2007套用大全(修訂版)
4.6.4 定義項目工作包 66 4.6.5 先建立WBS，再基於此定義項目日程 67 第5章 設定項目 68 5.1 定義項目信息 69 5.1.1 理解“項目信息”對話框 69 5.1.2 定義項目屬性 73 5.2 定義日曆 75 5.2.1 修改和定義基準日曆 76 5.2.2 設定項目日曆和資源日曆 80 5.3 定義自定義域 ...
- 漫畫線性代數
4.3 值域和定義域 4.4 滿射、單射、滿單射 4.5 逆映射 4.6 線性映射 5.希臘文字 6.理科特有的說法 7.排列組合 8.主將的命令和映射 第3章 矩 陣 1.矩 陣 2.矩陣的運算 3.特殊矩陣 第4章 矩陣(續)1.逆矩陣 2.逆矩陣的求解方法 3.行列式 4.求解行列式值的方法 5.利用代數餘子式的方法求逆...
- 哲學批判與解放的烏托邦
西方生態學馬克思主義的定義域與問題域 制度批判、技術批判、消費批判與生態政治哲學——西方生態學馬克思主義的核心論題 北美生態學馬克思主義對歷史唯物主義的重構 生態政治哲學何以可能——評西方生態學馬克思主義的生態政治哲學 文化、自然與生態政治哲學——詹姆斯·奧康納的生態學馬克思主義理論 生態唯物主義哲學的重建與...
- 經濟數學解題方法技巧歸納
1．1求幾類函式的定義域 1．2判斷兩函式是否為同一函式 1．3函式符號的幾點運用 1．4判別(或證明)函式的奇偶性 1．5判定函式的有界性 1．6判定函式在某區間上的單調性 1．7判定函式的周期性並求周期函式的周期 1．8三類反函式的求法 第2章 極限與連續 2．1用極限定義驗證某常數是函式的極限 2．2判別...
- 賈利娟
擔任《詩文選萃》1、2、3輯、《愛已成歌》《人生的定義域》《用生命敲擊世界》《德育讀本》《學海拾貝》等多本書的編委。個人撰寫的《誰言寸草心，報得三春暉》獲“中華民族傳統美德”論文評比特等獎。教學成果 擔任班主任工作十餘年，多次送畢業班，所教班級高考成績優異。獲市政府嘉獎。獲石家莊市青年教師優質...
- 王雨辰(中南財經政法大學教授)
4．《論西方生態學馬克思主義的定義域與問題域》，《江漢論壇》（CSSCI）2007年第7期；《中國社會科學文摘》2007年第6期全文轉載。5．《技術理性批判與科技倫理的重建：評威廉·萊斯的科技倫理價值觀》，《淮海工學院學報》，2007年第4期，《人大複印資料·倫理學》2008年第3期全文轉載。6．《現當代國外馬克思主義...
- MATLAB技術大全
6.3.1 定義域是無向的積分 198 6.3.2 對坐標的曲線積分和曲面積分 199 6.4 常微分方程和偏微分方程的求解 200 6.4.1 常微分方程的數值求解 200 6.4.2 偏微分方程的數值求解 204 6.5 本章小結 208 第7章 機率與統計 209 7.1 機率密度函式 210 7.1.1 連續分布密度函式 210 7.1.2 離散分布...
- 數學符號史(2006年9月科學出版社出版的圖書)
2.9.3 第三次擴張函式定義——科學函式的雛形 2.9.4 第四次擴張——現行國中函式定義的來源 2.9.5 第五次擴張（取消函式定義域的限制），第六次擴張 （近代定義）和第七次擴張（現代函式的定義）2.10 實數肩上的虛數 2.11 集合符號的春秋 2.12 代數的其他符號 2.12.1 絕對值符號｜｜ 2.12.2 ...
- Function(表示子例程的一般性名詞)
～‖函式的定義：設x和y是兩個變數，D是實數集的某個子集，若對於D中的每個值x，變數y按照一定的法則有一個確定的值y與之對應，稱變數y為變數x的函式，記作 y=f(x).數集D稱為函式的定義域，由函式對應法則或實際問題的要求來確定。相應的函式值的全體稱為函式的值域，對應法則和定義域是函式的兩個要素。
- 周學光(數學家)
這是多值的上同調運算，它的定義域為Y-系列上同調群的直和（Y，Hi（X）），而取值域為Y的上同調群Hn+1（Y，Hn+1（Xn）），其中Xn為X的高度為n的同調分解。周學光在該論文中利用特徵上同調運算得出了具有更高概括性的定理。定理指出，當X維數≤n+1或Y維數≤n+1且X單連通，則由X到Y的上同調系統中的...
- 編碼方法
②當真值為負數時，原碼、反碼和補碼的數符和數值均由定義直接求出，但在求定義域端點之值時，有時要對結果加以簡單處理。其符號是二進制為“1”，十進制為“9”。③當真值為二進制整數時，移碼才有定義移碼的數值部分與二進制整數補碼完全相同；符號則恰恰相反，即正數時為“1"，負數時為“0"。示例 已知二...
- 中國風格鋼琴音樂導論
演奏水平、欣賞水平等各方面都有很大的差距。20世紀以來國際音樂的現狀是令人憂思的。正如音樂理論學家彭志敏所言：“20世紀以來的現代音樂正面臨著這樣一個嚴峻的現實：音樂語言的定義域在被無限地擴大；表現方法的集合體在被無限地增元；‘個性超越’所導致的風格分化，其速度、其指數正在以料所不及的速率上升。
