低周疲勞

低周疲勞：又稱條件疲勞極限，或“低循環疲勞”。參照零件工作周期可能作用的次數下能承受的應力極限值。（可以有效發揮材料的作用）。

基本介紹

• 中文名：低周疲勞
• 外文名：Low cycle fatigue
• 別稱：條件疲勞極限
• 俗稱：低循環疲勞
• 作用：可以有效發揮材料的作用
• 類別：物理學

基本概念

疲勞

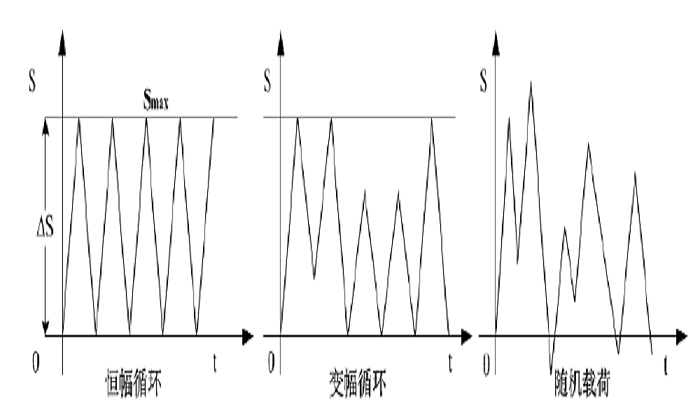
材料在循環應力和應變作用下，在一處或幾處逐漸產生局部永久性累積損傷，經一定循環次數產生裂紋或突然發生完全斷裂的過程。根據循環荷載的幅值和頻率，疲勞可以分為等幅疲勞、變幅疲勞和隨機疲勞;根據材料破壞前所經歷的循環次數(即壽命)以及疲勞荷載的應力水平，疲勞又可以分為高周疲勞、低周疲勞和亞臨界疲勞。

疲勞壽命

疲勞破壞時所經歷的應力、應變循環次數。

疲勞極限

指定基數下的中值疲勞強度，對當循環基數為其他值時，稱為該循環基數下的條件疲勞極限，有時簡稱為該循環基數下的疲勞強度。

疲勞累積損傷

譜荷載下疲勞損傷的積累。線性損傷時常用循環比的和表示，即D= ΣCi，其中Ci為第i級應力水平下的循環比。

疲勞破壞準則

疲勞破壞時應力空間或應變空間破壞包絡面的數學表達式。可供工程中疲勞計算分析時使用，但它不解決對疲勞破壞的物理和力學機理的認識。

S-N曲線

又稱應力一壽命曲線，是疲勞過程中所施加的應力水平與至破壞的循環次數即壽命之間的關係曲線。S代表應力水平，可以是循環過程中的最大應力、應力幅等，N表示壽命，可以用線性壽命，也可以用對數壽命。S-N曲線由德國人Wohler最先提出並使用，所以又被稱為Wohler曲線。通常所說的S-N曲線的N是具有50%的保證率的，即所謂的中值疲勞壽命。

研究歷史

有記載的最早的疲勞試驗是德國人W. A.艾伯特在1829年進行的。他對礦山提升用的焊接鏈反覆載入，在100000次循環後破壞。1839年，法國人J. V.彭賽列在他的著作中首次使用“疲勞”這個詞。1843年，蘇格蘭人W. J. M.蘭金討論來機車車軸的破壞，認為是由於運行過程中金屬性能逐漸變壞所致。他分析來車軸軸肩處尖角的有害影響，指出加大軸肩圓角的半徑可以提高其疲勞強度。與此同時，英國成立了一個委員會，調查用鐵作為建造鐵路橋樑的材料的適用性，在對梁進行了若干次試驗後指出，梁在靜載荷下可以承受接近破壞的載荷達四年之久而不破壞，但如用靜破壞載荷一半使梁反覆彎曲，只要1000次循環梁就破壞。足以表明疲勞破壞時，遠遠低於梁的極限載荷。

第一次對疲勞強度進行系統試驗的是德國人A.沃勒，他從1847年至1889年在斯特拉斯堡皇家鐵路工作期間，完成來循環應力下的多種疲勞試驗。1850年，他設計了旋轉疲勞試驗機，用來進行疲勞試驗，認識到疲勞破壞可以在應力低於彈性極限時發生，並存在一個應力幅極限值，當應力幅小於該值時就不會發生疲勞破壞。並且他首次提出S-N曲線及疲勞極限的概念。此外，他還研究來熱處理、應力集中和疊加靜載荷對疲勞的影響，對疲勞來講，應力幅要比平均應力更為重要。1884年J.包辛格在驗證A.沃勒的疲勞試驗時，發現“循環軟化”現象，當時並未引起人們的重視，直到1952年柯楊在做銅棒的疲勞試驗時才被重新提出來，並命名為“包辛格效應”。因此，J.包辛格是首先研究循環應力一應變關係的人。

1874年，W.格伯根據A.沃勒的試驗數據，對平均應力不為零的疲勞破壞以“極限”來表達，在任意給定壽命下都可畫出相應的疲勞極限線圖，即格伯拋物線。1930年，英國人J.古德曼對疲勞極限線圖提出簡化假設，即用直線連線縱軸上的對稱循環疲勞極限點和橫軸上的強度極限點，以此來代替格伯拋物線。

1903年，J. A.尤因和J. C. W.漢弗對鐵進行了旋轉彎曲疲勞試驗。在試驗過程中，用光學顯微鏡觀察式樣發現，在循環應力作用下晶體中產生滑移線，隨著循環數的增加，滑移線逐漸變深、變寬，形成滑移帶，並在某個晶體上首先出現開裂，再在晶體之間連線起來形成一條長的連續的裂紋，最後導致破壞。

1923年，英國人H. J.高夫對疲勞理論提出來另一種假設。他認為在應力幅低於疲勞極限，將不產生塑性變形;如應力幅高於疲勞極限，應變硬化將達到一個極限值，從而形成裂紋。

1945年美國人M. A.邁因納在J. V.帕姆格倫工作的基礎上重新提出:損傷與應力循環數成線性關係，後人稱為MINER準則。1974年美國學者J. W.費舍爾通過大量足尺寸焊接疲勞試驗結果證明，影響疲勞的主要因素是應力幅，而不是最大應力和應力比。

常規疲勞強度設計中假設材料是無缺陷的連續體，疲勞破壞的過程分為裂紋形成、裂紋擴展和最後斷裂三個階段。但實際上材料中總是存在著裂紋的缺陷，因此，斷裂損傷力學理論套用於疲勞強度設計是未來發展的趨勢，在1920年，英國人A. A.格里菲斯研究來玻璃的實際強度要比它的分子結構所預期的理論強度低一千倍到一萬倍的現象，他對帶裂紋玻璃平板的斷裂研究標誌著現代斷裂損傷理論的開始，可是一直沒有可進行定量處理有關疲勞破壞模型的數學框架，直到1957年美國人P. C.帕里斯提出，在循環荷載作用下，裂紋尖端的應力強度因子幅值是控制構件疲勞裂紋擴展速率的基本參量，並於1963年提出來指數冪定律帕里斯公式。

1960年，低周應變疲勞性能的研究得到發展，L. F.克里夫和S. S.瑪森各自獨立提出來塑性應變幅和疲勞壽命之間的經驗關係，進而形成局部應力應變法。1968年，非線性斷裂損傷力學的研究有了新起點，R工CE提出來與路徑無關的J積分，並且發表來著名的HRR彈塑性靜止裂紋尖端奇異解，標誌這彈塑性斷裂力學理論開始走向成熟。基於斷裂力學目前己發展來一種損傷容限方法，疲勞設計和壽命分析的斷裂力學方法，或許成為以後的主導。1977年，美國的鋼結構、鐵路鋼橋、公路橋樑三個設計規範同時改版，並且都是採用應力幅值作為疲勞驗算的抗力。

近20年來，疲勞研究在我國得到跨越式發展，相對國外而言，我國疲勞研究起步較晚，從1950年初開始，80年代得到來發展，就研究內容來說，與國外相比研究的重點不同。壽命估算和隨機疲勞成為我國研究的熱點問題。

總之，疲勞理論經過無數研究者的不斷完善，逐步形成了比較系統的研究理論，隨著電子計算機的發展，運用軟體分析和模擬疲勞裂紋的發展，將成為未來研究的主導，通過計算機的模擬計算，進行疲勞壽命的估算。從而為鋼橋的疲勞評估，找到有效的方法。

分析方法

傳統分析方法

傳統的疲勞分析方法主要以S-N曲線和Miner線性累積損傷準則為基礎，通過計算來評估橋樑的疲勞壽命。傳統疲勞分析方法在鋼橋的套用主要是解決疲勞細節分類和確定荷載效應這兩個問題上。

S-N曲線是材料作用應力S與破壞時的壽命N之間關係曲線。在對數坐標系下，S-N曲線在大部分的範圍內為線性關係。通過分析載荷譜，按照一定的損傷累積法則來計算預測構件的疲勞壽命，S-N曲線以疲勞試驗為基礎，具有較好的可靠度，因此在橋樑上得到廣泛的套用。在得出了鋼橋結構的應力時間歷程後，為了獲得應力幅的變化情況，一般採用循環統計計數方法進行分析，可以得到不同的應力幅及相應的應力幅循環次數，通常使用的循環統計計數方法包括普通計數法、功率譜法、雨流計數法、泄水池法。一般工程使用的都是雨流計數法。

傳統疲勞分析方法主用利用S-N曲線方法，分析形式簡單，而且很多國家都針對自己的實際情況，制定了詳細的疲勞荷載譜，操作比較方便，套用比較廣泛，但如何獲得複雜結構的S-N曲線和有關部位的應力歷程是重點。

基於斷裂力學的分析方法

傳統的疲勞分析方法假定結構沒有裂紋，分析的是從裂紋產生到擴展，直至結構破壞的全過程。斷裂力學疲勞分析方法認為任何材料都存在缺陷，疲勞裂紋則來源於這些原始缺陷，而構件的破壞是在交變載荷的作用下疲勞裂紋擴展的結果。斷裂力學分析方法承認初始缺陷的存在，更加符合實際情況，對於己經使用的鋼橋累積損傷及疲勞壽命的評估具有重大意義。通過獲得初始裂紋尺寸、臨界裂紋尺寸、相應的應力強度因子表達式和材料的疲勞裂紋擴展速率表達式，就能對結構的剩餘疲勞壽命進行估算。

工程上套用最廣泛的疲勞裂紋擴展速率公式是Paris公式，兩個裂紋擴展參數C和M為隨機變數。在鋼橋套用上，許多研究人員根據結構具體情況得到了相應的C和m值。應力強度因子和斷裂判據是斷裂力學最重要的問題。應力強度因子的計算目前主要有解析法和數值法，解析法主要包括應力函式法、積分變換法、奇異積分方程法、權函式法等;數值方法有J積分法、虛裂紋閉合法、位移相關法。由於有限元方法不受裂紋體幾何及載荷形式的限制，對於結構或裂紋形狀複雜和受複雜載荷作用的結構比較適用，對於在斷裂理論中得到比較好的套用。基於斷裂理論的研究方法，己經形成了適用的壽命評估方法，如損傷容限方法。即先用無損探傷技術確定初始的微裂紋，在沒有發現微裂紋的情況下，則利用探傷技術中的擬定微裂紋的初始尺寸，最後通過斷裂力學研究微裂紋的擴展規律，並預測結構的剩餘壽命，並確定下一次檢測的時間間隔。當達到檢測時間間隔時應重新進行相應的檢測，根據新的檢測結果重新計算剩餘壽命和檢測間隔，以此循環下去，直至鋼橋達到必要的加固狀態。

運用斷裂力學來分析鋼橋疲勞問題是目前發展較快的領域，雖然大部分國家仍然沿用傳統疲勞分析方法，但越來越多的研究人員致力於運用斷裂力學方法來分析鋼橋的疲勞破壞，在橋樑中確定了臨時構造細節，經無損檢測得到初始裂紋的長度，通過對Paris公式進行積分，得到該構造細節的疲勞壽命。
基於斷裂力學的疲勞分析方法在實際工程問題中，一般構件的受力情況是複雜的，裂紋的位置和擴展的方向受到各種因素的影響，裂紋尖端實際多處於複合型受力狀態，為解決複合型裂紋起裂條件和擴展方向，需要建立準確的斷裂依據。但是由於複雜結構應力強度因子的計算是其難點，而且工程上套用較廣泛的Paris公式只考慮了裂紋擴展階段，套用斷裂力學獲得裂紋的全壽命計算模型是其難點。

損傷力學的分析方法

損傷力學疲勞分析方法是研究含損傷材料在變形過程中損傷的不斷演化直至發展到破壞的應力應變過程的方法。損傷力學理論認為結構在初始狀態時就存在損傷，構件承受荷載過程中，這些損傷是不斷的演化發展的，而且具有不可逆性，當損傷達到一定閥值時，結構就發生了破壞。損傷力學發展20多年的歷史，但己經發展演化出了兩個平行的分支，連續損傷力學和細觀損傷力學。損傷力學的發展為疲勞分析提供了新的概念和分析方法，傳統的疲勞分析方法中未引入損傷的概念，然而在疲勞過程中，應力、應變、剛度是不斷變化的，因此無法獲得整個疲勞過程中力學行為的描述，同時從疲勞裂紋形成到裂紋擴展是一個連續的變化過程，而傳統疲勞分析方法卻把其分為兩個獨立的時期來研究，套用不相同的計算方法和分析方法。但是在套用損傷理論之後，科研人員利用連續損傷場的概念，解釋了金屬材料中的位錯與微裂紋等內部缺陷，對金屬本構關係的重要影響，從熱力學原理中的不可逆理論中，建立了損傷動力學與損傷力學本構關係的模型。損傷力學可以有效地降低疲勞分析對實驗的依賴程度，也可將疲勞裂紋形成與裂紋擴展兩個階段統一在損傷力學理論框架下進行分析和描述，可對整個疲勞過程中的力學行為進行數值模擬計算。

損傷力學分析方法中，通常用損傷因子D作為特徵參量去描述結構的損傷速率dD/dN，從能量和微觀的角度分析疲勞的產生和擴展的過程。但是損傷力學出現的時間不長，工程界對疲勞損傷因子的定義還沒有統一的認識，損傷演化模型也不完善，沒有工程實例作為支撐，同時由於其分析方法的獨特，可以肯定未來套用前景廣大。

分類

為便於分析研究，常按破壞循環次數的高低將疲勞分為兩類：

①高循環疲勞（ HCF，高周疲勞）。作用於零件、構件的應力水平較低 ，破壞循環次數一般高於10^4的疲勞 ，彈簧、傳動軸等的疲勞屬此類。

②低循環疲勞（LCF，低周疲勞）。作用於零件、構件的應力水平較高 ，破壞循環次數一般低於10^3～10^4的疲勞，如壓力容器、燃氣輪機零件等的疲勞。實踐表明，疲勞壽命分散性較大，因此必須進行統計分析，考慮存活率（即可靠度）的問題 。具有存活率p（如95%、99%、99.9%）的疲勞壽命Np的含義是 ：母體（總體）中有p的個體的疲勞壽命大於Np。而破壞機率等於（ 1－ p ） 。常規疲勞試驗得到的S-N曲線是p=50%的曲線 。對應於各存活率的p的S-N曲線稱為p-S-N曲線。

高周疲勞是材料所受的最大交變應力遠低於材料的極限強度，甚至只有極限強度的二分之一左右，破壞前的循環次數大於10³次，通常用S-N曲線描述材料高周疲勞特性。低周疲勞是指材料所受的應力水平較高，通常接近材料的極限強度，斷裂前循環次數較少，一般少於10³，每次循環中塑性變形較大，低周破壞是塑性變形累積的結果，因此又把低周疲勞稱為塑性疲勞。地震波荷載常用低周疲勞過程來模擬。由於低周疲勞壽命N對於應力水平S的變化過於敏感，用S-N曲線已不足以描述起疲勞性能，常用￡-N描述其疲勞性能。當疲勞應力水平很小時，
疲勞壽命會很大，我們把這種情況稱為亞臨界疲勞。把疲勞分為低周疲勞、高周疲勞和亞臨界疲勞是有明確的現實意義的，對於低周疲勞，由於模擬的是地震波荷載，並且實驗驗證比較容易，受到人們的普遍重視，並已取得相當成效;對於亞臨界疲勞，由於人力、物力、財力資源的限制，很難用實驗手段對其性能進行研究，現在的研究只限於理論研究階段，或者把已進行的高周疲勞實驗結果適當外延，用於亞臨界疲勞;高周疲勞介於二者之間，對應較多實際工程中構件的受力狀態，正逐步引起人們的注意，並已取得一定成效。