基本介紹
- 中文名:位流
- 外文名:Irrotational flow
- 別名:非旋轉流
- 領域:空氣動力學
- 特點:位流的渦流為0
- 性質:矢量
非正式表達
 路徑依賴
路徑依賴直觀解釋
定義
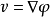
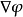
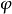
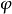
位流

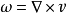

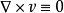

 路徑依賴
路徑依賴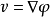
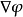
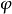
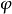

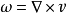

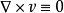
位流,也叫非旋轉流。在矢量運算中,保守向量場是一個矢量場,它是一些函式的梯度。保守矢量場具有線積分是路徑無關的特點,即兩點之間的任何路徑的選擇不會改變線...
位勢流(Potential Flow)又稱位流,勢流。它的流場是一個標量函式Φ的梯度。採用直角坐標系x、y、z,把流速U的三個分量用u,v,w來表示,則它們都是x、y、z和...
單個位測試(monobit test)是指:測試一個二進制位流,如果1和0的個數大致相等,則此位流通過了單個位測試。...
數碼信號:H.264格式,寬高比16:9,DMB-T/H制式,音效以杜比AC-3編碼,一般傳送兩條AC-3位流,每位流一般為兩聲道。 注:2012年7月26日起,數碼信號國際台改為...
JBits由一系列的Java類庫組成,可以控制位流配置數據的產生,並提供了能夠直接訪問Xilinx Virtex-II(tm) FPGA晶片位流結構檔案的應用程式接口(API)。...
徑流模數 [1] 是單位流域面積上單位時間所產生的徑流量。單位立方米/秒*平方千米。在所有計算徑流的常用量中,徑流模數消除了流域面積大小的影響,最能說明與自然...
利用這些工具,用戶可以方便地從多媒體資料庫中有選擇地獲取自己所需的與對象有關的內容,並提供了內容的操作和位流編輯功能,可套用於互動式家庭購物,淡入淡出的數字...
名稱同步通信Synchronous Communication 簡介 當兩台設備交換數據時,它們之間存在一個信息流,叫位流(bit-stream)。任何一種數據傳輸中,傳送者和接收者都必須有一個...
傳送緩衝器(TXB)是CPU 和位流處理器(BSP)之間的接口,負責存儲傳送到CAN匯流排上的一條完整的報文。傳送緩衝器的長度為13個位元組,由CPU寫入、位流處理器讀出。...
