伯努利不等式,又稱貝努利不等式,是分析不等式中最常見的一種不等式,由數學家伯努利提出。
基本介紹
- 中文名:伯努利不等式
- 外文名:Bernoulli inequality
- 注意:注意前提、等號成立條件
- 發明人:伯努利(Bernoulli)
- 適用學科:高等數學
- 又名:貝努利不等式
基本概念,證明,相關不等式,
基本概念
對實數x>-1,
在 時,有
時,有 成立;
成立;


在 時,有
時,有 成立。
成立。


可以看到等號成立若且唯若n = 0,1,或x = 0時。
伯努利不等式經常用作證明其他不等式的關鍵步驟。
伯努利不等式的一般式為

(對於任意 都有
都有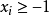 且
且 ,即所有
,即所有 同號且大於等於-1) 若且唯若n=1時等號成立
同號且大於等於-1) 若且唯若n=1時等號成立

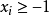


證明
設x>-1,且x≠0,n是不小於2的整數,則(1+x)^n≥1+nx。
證明:
先證明對所有正整數不等式成立。用數學歸納法:
當n=1,上個式子成立,
設對n-1,有:
(1+x)^(n-1)>=1+(n-1)x成立。
則
(1+x)^n
=(1+x)^(n-1)(1+x)
>=[1+(n-1)x](1+x)
=1+(n-1)x+x+(n-1)x^2=1+nx+nx^2-x^2
>=1+nx
就是對一切的自然數,當
x>=-1,有
(1+x)^n>=1+nx
若r ≤0或r ≥ 1,有(1+x)^r ≥ 1 + rx
若0 ≤ r ≤ 1,有(1+x)^r ≤ 1 + rx
這個不等式可以直接通過微分進行證明,方法如下:
如果r=0,1,則結論是顯然的
如果r≠0,1,作輔助函式f(x)=(1+x)^r-(1+rx), 那么f'(x)=r*(1+x)^(r-1)-r, 則f'(x)=0 <==> x=0;
下面分情況討論:
2. r < 0或r > 1,則對於x > 0,f'(x) > 0;對於 − 1 < x < 0,f'(x) < 0。嚴格遞減,因此f(x)在x = 0處取最小值0,故得(1+x)^r ≥ 1+rx
證畢。
相關不等式
下述不等式從另一邊估計 :對任意
:對任意 ,都有
,都有



我們知道 ( x>0),因此這個不等式是平凡的。
( x>0),因此這個不等式是平凡的。