任意子是數學和物理學中的一個概念。它描述一類只在二維系統中出現的粒子。它是對費米子和玻色子概念的廣義化。
基本介紹
- 中文名：任意子
- 套用：物理，數學
- 相關理論：費米子和玻色子概念
- 範圍：二維系統
物理學,拓撲學基礎,費米子,玻色子,
物理學
在石墨烯、量子霍爾效應等二維物理系統中任意子這個數學概念變得越來越有用。 在三維以上的空間裡，粒子根據其統計特性的不同只能是費米子或者是玻色子。費米子遵從費米-狄拉克統計，玻色子遵從玻色-愛因斯坦統計。在量子力學中這些統計是根據多粒子狀態下粒子交換的反應來描寫的。使用狄拉克符號在兩粒子狀態中為：
其中
中的第一項是第一個粒子的狀態，第二項是第二個粒子的狀態。因此公式的左側的意思是“粒子一在
狀態和粒子二在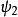
狀態”。加號相應於兩個粒子都是玻色子，減號相應於兩個粒子都是費米子（玻色子和費米子混合的狀態是不可能的）。
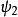
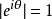
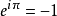
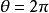
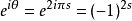
在邊界上，分數量子霍爾效應任意子被限制在一維空間中移動。一維任意子的數學模型提供了上述交換關係的基礎。
拓撲學基礎
在任何二維以上的空間裡，自旋統計定理規定任何多粒子狀態都必須要么遵循費米-狄拉克統計，要么遵循玻色-愛因斯坦統計。這與{\displaystyle n>2}的SO(n,1)基本群有關，其值為{\displaystyle \mathrm {Z} _{2}}（有兩個元素的循環群）。因此這裡只有兩個可能性（這裡的細節比上述的要複雜，但是最關鍵的原因是這個）。
在二維空間裡情況發生了變化，這裡SO(2,1)的基本群是{\displaystyle Z}（無限循環）。這意味著自旋（2，1）不是通用覆蓋：它們不是單連通。詳細地說特殊正交群SO(2,1)的射影表示不僅僅有SO(2,1)或者其二重複蓋群旋量群自旋（2，1）的線性表示。而這些額外的表示被稱為任意子。
這個概念對非相對論系統也有效。關鍵是空間旋量群是有無限基本群的SO(2)。
這個事實也與紐結理論中著名的辮群有關。在二維中兩個粒子的排列群不再是對稱群{\displaystyle S_{2}}，而是辮子群{\displaystyle B_{2}}了。這樣也可以來理解這個問題。
有一種考慮解決量子計算機中的穩定性問題的方法是使用任意子製成的拓撲量子計算機。這種計算機使用準粒子作為執行緒，使用辮理論來設計穩定的邏輯門。
費米子
費米子可以是基本粒子，例如電子，或者是複合粒子，例如質子、中子。根據相對論性量子場論的自旋統計定理，自旋為整數的粒子是玻色子，自旋為半整數的粒子是費米子。除了這自旋性質以外，費米子的重子數與輕子數守恆。因此，時常被引述的“自旋統計關係”實際是一種“自旋統計量子數關係”。
根據費米-狄拉克統計，對於N個全同費米子，假設將其中任意兩個費米子交換，則由於描述這量子系統的波函式具有反對稱性，波函式的正負號會改變。由於這特性，費米子遵守包利不相容原理：兩個全同費米子不能占有同樣的量子態。因此，物質具有有限體積與硬度。費米子被稱為物質的組成成分。質子、中子、電子是製成日常物質的關鍵元素。
玻色子
在量子力學里，粒子可以分為玻色子（英語：boson）與費米子。保羅·狄拉克為了紀念印度物理學者薩特延德拉·玻色的貢獻，因此給出玻色子的命名。玻色與阿爾伯特·愛因斯坦合作發展出的玻色-愛因斯坦統計可以描述玻色子的性質。在所有基本粒子中，標準模型的幾個傳遞作用力的規範子，光子、膠子、W玻色子、Z玻色子都是玻色子，賦予基本粒子質量的希格斯子是玻色子，已被證實。在量子引力理論里傳遞引力的引力子也是玻色子，尚未被證實存在。在複合粒子裡，介子是玻色子，質量數為偶數的穩定原子核，像重氫H（原子核由一顆質子和一顆中子組成，質量數為2）、氦-4、鉛-208等也是玻色子，準粒子像庫柏對、等離體子、聲子等都是玻色子。
