射影表示是與相應射影線性群密切相關的一種表示。
當K為特徵0的代數封閉域時,有限群G的不可約射影示的次數為G的階的因子。
基本介紹
- 中文名:射影表示
- 外文名:projective representation
- 適用範圍:數理科學
定義
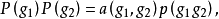
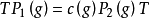
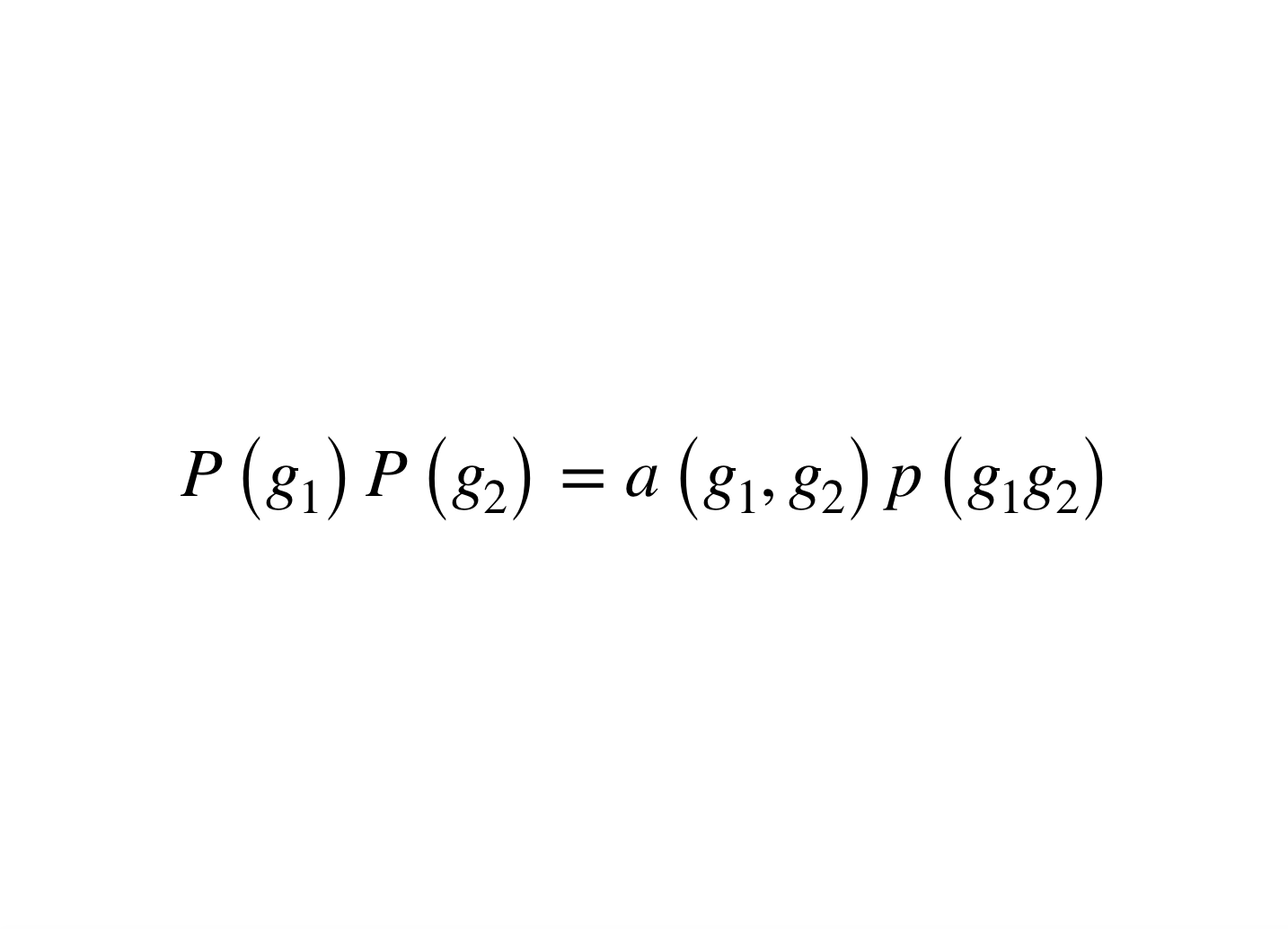
射影表示是與相應射影線性群密切相關的一種表示。
當K為特徵0的代數封閉域時,有限群G的不可約射影示的次數為G的階的因子。
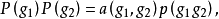
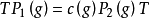
射影表示是與相應射影線性群密切相關的一種表示。當K為特徵0的代數封閉域時,有限群G的不可約射影示的次數為G的階的因子。...
射影是一個存在於數學及物理學中的概念,存在於集合論、線性代數、幾何學以及拓撲學等諸多理念中。在平面幾何中,與一個圖形相似的圖形叫做這個圖形的射影。射影是...
射影對應是射影幾何中最重要的一種對應,通常指射影空間(平面、直線)之間保持共線性和共線四點的交比不變的點的一一對應。當兩個對應的射影空間(平面、直線)...
射影定理,又稱“歐幾里德定理”:在直角三角形中,斜邊上的高是兩條直角邊在斜邊射影的比例中項,每一條直角邊又是這條直角邊在斜邊上的射影和斜邊的比例中項...
射影幾何是研究圖形的射影性質,即它們經過射影變換後,依然保持不變的圖形性質的幾何學分支學科。也叫投影幾何學,在經典幾何學中,射影幾何處於一個特殊的地位,...
在歐幾里得直線上添加一個無窮遠點後,所得的直線稱為擴大直線或仿射直線。若在擴大直線上,對無窮遠點和有窮點不加區別,同等看待,則稱這樣的擴大直線為射影直線,...
直角三角形射影定理,又稱“歐幾里德定理”,定理內容是直角三角形中,斜邊上的高是兩直角邊在斜邊上射影的比例中項,每一條直角邊是這條直角邊在斜邊上的射影和...
射影角度(projective angular measure)是射影幾何的一個術語,指射影幾何中所定義的兩條直線的夾角。例如,在射影平面上取定一個非退化的二級曲線,另選定一個常數...
由有限次中心射影的積定義的兩條直線間的一一對應變換稱為一維射影變換。由有限次中心射影的積定義的兩個平面之間的一一對應變換稱為二維射影變換。因為正交變換...
射影平面就是2維射影空間。它可以視為平面添上一條無窮遠直線。 它是代數幾何、射影幾何里最基本的對象。對射影平面的理解是從局部到整體的擴展過程。先從無窮...
含沙射影是一個漢語成語,拼音是hán shā shè yǐng,意思是傳說一種叫蜮的動物,在水中含沙噴射人的影子,使人生病。比喻暗中攻擊或陷害人。...
一維射影對應(one-dimensional projective correspondence)是透視對應的推廣,兩個一維基本形(點列或線束)間的一一對應是射影對應的充分必要條件是任何四元素的交比...
射影性質是射影變換的一種特徵,指圖形經過任何射影對應(變換)都不變的性質,例如,非調和比、二次曲線極點與極線的關係、一條代數曲線的類型或階、同素性、結合...
定義1.如圖,已知∠AOB∈(0,π),設A,O,B在平面α上的射影分別為A′,O′,B′,且A′,O′,B′不共線,則稱∠A′O′B′是∠AOB在平面α上的射影角(...
射影距離(projective distance)是射影幾何的一個術語,指射影幾何中所定義的兩點之間的距離。例如在射影平面上取定一個非退化的二階曲線,若取一個常數k(k≠0)...
Pn(C)的一個子集,若它可以表示為定義在Cn+1中一組齊次多項式公共零點的集合,則稱它為射影代數簇,簡稱代數簇,也可稱它為Pn(C)的代數子集。...
含莎射影內容簡介 編輯 霧散,夢醒,她看見了真實,是五年後千帆過盡的沉寂。 一場絢麗的愛慕已至荼靡。 五年前,一個隨意丟棄的蘋果砸出一場煙花般的愛慕,演...
射影幾何是研究圖形的射影性質,即它們經過射影變換後,依然保持不變的圖形性質的幾何學分支學科。射影幾何學也叫做投影幾何學。在經典幾何學中,射影幾何處於一種...
若V是K上n維右向量空間,P(V)是V的全體一維子空間的集合(即射影空間),則由...實數域和複數域上的典型群是李群的重要例子,它們的構造及表示在李群理論、幾何...
在幾何學裡,球極平面射影是一種將一個圓球面射影至一個平面的映射。 ...... 在幾何學裡,球極平面射影是一種將一個圓球面射影至一個平面的映射。...
