基本介紹
- 中文名:亥姆霍茲函式
- 外文名:Helmholtz function
- 領域:熱力學
- 類型:熱力學參數
- 別名:亥姆霍茲自由能
- 條件:封閉系統
簡介,定義,亥姆霍茲函式判據,物理意義,
簡介
在熱力學中,亥姆霍茲自由能是一個熱力學勢,用在恆定的溫度和體積下從封閉熱力系統能得到的最大“有用”功。 對於這樣一個系統,亥姆霍茲能差值的負數等於溫度和體積保持不變下可逆等溫過程的最大功輸出。 在這種條件下,在其最小值時為熱力學平衡狀態。亥姆霍茲自由能是由赫爾曼.馮.亥姆霍茲(Hermann von Helmholtz)提出,通常由字母A(從德語"Arbeit ”或功)或字母 F表示。 國際理論和套用化學聯合會(IUPAC)建議使用字母 A,並建議使用亥姆霍茲能作為名稱。在物理學中,常用字母F來表示亥姆霍茲能,這是通常稱為亥姆霍茲函式或簡稱為“自由能”。
儘管吉布斯自由能(Gibbs free energy)是最常用的一種用來度量熱力學勢的方法,特別是在化學領域中,一些場合的等壓的限制導致套用的不便。 例如,在爆炸的研究中,因為爆炸反應有引起壓力變化的本質特性而經常使用亥姆霍茲自由能。它也經常被用來在精確的熱力學性質關係式中定義純物質狀態方程基本狀態方程。
定義


故:  (1)
(1)

這個過程一定也滿足熱力學第一定律:
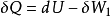

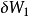

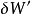
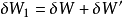
將式(1)代入上式得:


定溫下:
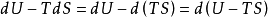

定義:
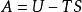

對有限量過程:
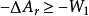
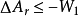
式中: 稱為亥姆霍茲函式。由式(2)~式(4)可得兩點有意義的結論:
稱為亥姆霍茲函式。由式(2)~式(4)可得兩點有意義的結論:

(1)亥姆霍茲函式 是狀態函式,具有能量的量綱。因
是狀態函式,具有能量的量綱。因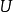 的絕對值無法確定,所以
的絕對值無法確定,所以 的絕對值也無法確定。
的絕對值也無法確定。 是容量性質。
是容量性質。

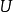


(2)對可逆過程, ,式(4)可寫作
,式(4)可寫作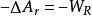 ,該式表明了亥姆霍茲函式
,該式表明了亥姆霍茲函式 的物理意義為:系統在定溫條件下對外做的最大功(
的物理意義為:系統在定溫條件下對外做的最大功( 包括體積功
包括體積功 和非體積功
和非體積功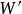 )等於系統的亥姆霍茲函式的減少(
)等於系統的亥姆霍茲函式的減少(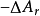 )。
)。

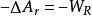



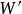
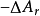
亥姆霍茲函式判據
(1)定溫條件下的 判據。由式(4)可知:
判據。由式(4)可知:

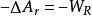

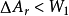

(2)定溫定容條件下的A判據。定容條件下,體積功W=0,所以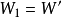 ,式(4)寫為:
,式(4)寫為:
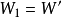
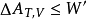


(3)定溫定容且不做非體積功條件下的A判據。因為系統不做非體積功, ,
, ,式(4)寫為:
,式(4)寫為:





因為可逆過程中每個狀態無限接近平衡態,所以也可以用 判斷系統處於平衡狀態。
判斷系統處於平衡狀態。

式(5)表明,在定溫定容且不做非體積功的條件下,封閉系統中發生的不可逆過程總是朝著A減少的方向進行,直到系統的A達到最小值,此時系統就達到平衡狀態。達平衡態後系統進行可逆過程A值不變。
物理意義
由A的定義有

恆溫時

將熱力學第一定律套用於可逆過程,即 ,代入上式,得
,代入上式,得


即恆溫過程系統亥姆霍茲函式的增量等於過程的可逆功。而過程恆溫可逆進行時,系統對環境作的功最大,可逆功形,表示系統所具有的對外作功的能力,故 ,反映了系統進行恆溫狀態變化時所具有的對外作功能力的大小。
,反映了系統進行恆溫狀態變化時所具有的對外作功能力的大小。

式(6)右邊可逆功 ,應為可逆體積功
,應為可逆體積功 與可逆非體積功
與可逆非體積功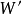 之和,代人式(6)有
之和,代人式(6)有


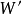

若過程除恆溫以外,且恆容,即 ,則有
,則有


此式表明,恆溫恆容過程系統亥姆霍茲函式的增量表示系統所具有的對外作非體積功的能力。



