高等工程熱力學中，表示系統基本熱力學關係的微分方程。表征內能、熱力學焓、亥姆霍茲自由能、吉布斯自由能
由熱力學的基本微分方程可得：dU=TdS-pdV (1)
由H=U+pV可得:dH=TdS+Vdp (2)
由F=U-TS可得:dF=-SdT-pdV (3)
由G=F+pV可得:dG=-SdT+Vdp (4)
基本介紹
- 中文名：熱力學函式的全微分
- 外文名：Complete differentials of Thermodynamic Functions
- 套用學科：熱力學、統計物理、工程熱力學
- 適用領域範圍：換熱計算、強化傳熱、流體傳熱
正文,
正文
對於封閉系統，將熱力學第一定律與熱力學第二定律相結合，可以得到如下一組關係式：
dU=TdS-pdV (1) dH=TdS+Vdp (2) dA=-SdT-pdV (3) dG=-SdT+Vdp (4)
式中為內能；為焓；為亥姆霍茲函式；為吉布斯函式；為熵；為熱力學溫度；為體積；為壓力。這一組關係式就稱為封閉系統的熱力學函式基本關係式。式(1)～(4)只適用於內部平衡且不做非體積功的封閉系統。
利用上述基本關係式的積分，可以求得一個封閉系統經歷一個任意可逆過程後狀態函式的變化。對於只由兩個獨立變數便可描述的封閉系統（即沒有不可逆的化學變化和相變化的封閉系統），上述基本關係式實際上可看作狀態函式、、和的全微分表達式。無論過程是否可逆，它們的積分都存在，且只由系統的始、終態決定。因此，對這樣的系統，不可逆過程的狀態函式的變化，也可由上述基本關係式積分求得。
利用封閉系統的熱力學基本關係式，還可以推導出許多重要的關係式。例如，從式(1)～(4)可導出：
T=(дU/дS)V=(дH/дS)p (5) p=-(дU/дV)S=-(дA/дV)T (6) V=(дH/дp)S=(дG/дp)T (7) S=-(дA/дT)V=-(дG/дT)p (8)
利用數學上的全微分性質，還可由式(1)～(4)導出：
(дT/дV)S=-(дp/дS)V (9) (дT/дp)S=(дV/дS)p (10) (дS/дV)T=(дp/дT)V (11) (дS/дp)T=-(дV/дT)p (12)
式(9)～(12)稱為麥克斯韋關係式組。利用此關係式,可把一些實驗上難以測量的量〔如(д/д)〕轉化為易於測量的量〔如(д/д)〕。
利用麥克斯韋關係式，可從式(1)和(2)導出：
(дU/дV)T=T(дp/дT)V-p (13) (дH/дp)T=-T(дV/дT)p+V (14)
式(13)、(14)描述了系統的內能和焓隨系統的體積和壓力的變化關係，通常稱為熱力學狀態方程。
對化學組成可變的均相系統，式(1)～(4)可改寫為：
(15) (16) (17) (18)
式(15)～(18)稱為開放系統的熱力學函式基本關係式。式中為系統中物質B的化學勢;d為物質B的物質的量的微小變化值。
如果系統在變化過程中除體積功和化學功外還有其他功（如電、磁、表面功等），則熱力學函式基本關係式的形式為
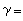熱力學函式基本關係式
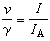熱力學函式基本關係式
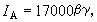熱力學函式基本關係式
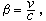熱力學函式基本關係式(19) (20) (21) (22)
式中′為除體積功以外的其他功。
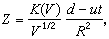熱力學函式基本關係式
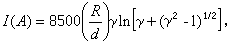熱力學函式基本關係式
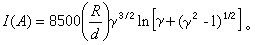熱力學函式基本關係式
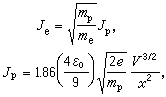熱力學函式基本關係式