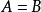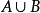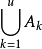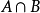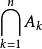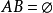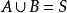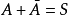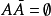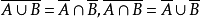事件亦稱隨機事件,機率論的基本概念之一,是隨機現象的表現,是由某些基本事件構成的集合。事件一般用大寫字母A,B,C,...表示,稱事件A發生,若且唯若A中所含的某一基本事件發生。在每次隨機試驗中一定會出現的事件稱為必然事件,用Ω表示;在任何一次試驗中都不會出現的事件稱為不可能事件,用∅表示。例如,投擲一枚骰子,觀察所出現的點數,A:“擲出偶數點”,B:“擲出的點數小於3”都是事件,而“擲出的點數小於7”是必然事件,“擲出的點數大於6”是不可能事件,如果事件A的發生必然導致事件B的發生,或者組成事件A的樣本點都是組成事件B的樣本點,則稱事件B包含事件A,記為A⊂B或B⊃A,顯然有∅⊂A⊂Ω,如果A⊂B與B⊂A同時成立,則稱事件A與B相等或等價,記為A=B。
基本介紹
- 中文名:事件
- 全稱:隨機事件
- 屬性:機率論的基本概念之一
- 舉例:拋一枚硬幣、玩骰子等
基本介紹
知識儲備

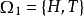
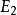


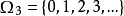


定義


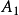
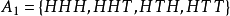








事件間的關係