不可微函式是指那些在定義域中有些點不存在導數的函式。
基本介紹
- 中文名:不可微函式

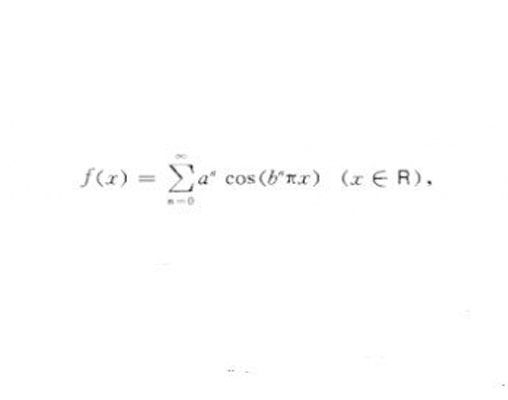
不可微函式是指那些在定義域中有些點不存在導數的函式。

不可微函式是指那些在定義域中有些點不存在導數的函式。...... 中文名 不可微函式 不可微函式(non-differentiable function)微分不存在的函式.若一元函式f在二...
在微積分學中,可微函式是指那些在定義域中所有點都存在導數的函式。可微函式的圖像在定義域內的每一點上必存在非垂直切線。因此,可微函式的圖像是相對光滑的,...
對線性約束的情形,當ƒ(f)為可微凸函式時有三種較為有效的求的算法:G.藻滕代克於1960年提出的可行方向法, 取=y(k)- f(k),其中y(k)為ƒ(f)在 f...
函式的連續性、可導性、可微性是高等數學中的重點和難點內容。一元函式可微與存在導數是等價的。而對於多元函式,偏導數即使都存在,該函式也不一定可微。...
設函式y= f(x),若自變數在點x的改變數Δx與函式相應的改變數Δy有關係Δy=A×Δx+ο(Δx),其中A與Δx無關,則稱函式f(x)在點x可微,並稱AΔx為...
光滑可微函式(smooth and differentiable function) 既是光滑又是可微的函式,簡稱為光滑可微函式。...
在計算機語言或計算器中,絕對值函式常記作abs(x) 。(1)絕對值函式是偶函式,其圖形關於y軸對稱。(3)絕對值函式僅在原點不可微,其他點處可微。...
函式論,含義是實變函式論和復變函式論的總稱,實函式論是研究函式的連續性、可微性和可積性的理論;復變函式論是研究復變數的解析函式性質的理論。以實數作為...
ζ 函式[3] (ζ-function)是用來刻畫系統周期點性態的函式。設M是微分流形,f:M→M是可微映射,對m=1,2,...,記Nm=Nm(f)為fm的不動點數目。假設Nm<+...
函式組(作為向量空間內的向量組)的線性相關概念的推廣.設.ft },fz,...,,fm是定義在區域DcR”上的n元連續函式,若存在k及可微函式F,使對任意xED,有.fk}x...
《奇異積分和函式的可微性》是 2011年 世界圖書出版公司出版的圖書,作者是(美國)施泰恩(SteinE.M.) 。...
可微的充要條件是曲面z=f(x,y)在點P(x0,y0,f(x0,y0))存在不平行於z軸的切平面Π的充要條件是函式f在點P0(x0,y0)可微....
令函式是在開區間上可微的,若函式的導函式是開區間上的連續函式,則稱函式在開區間上連續可微,記作連續可微。...
區域上處處可微分的復函式。17世紀,L.歐拉和J.leR.達朗貝爾在研究水力學時已發現平面不可壓縮流體的無旋場的勢函式Φ(x,y)與流函式Ψ(x,y)有連續的偏導數,...
光滑函式(smooth function)是指在其定義域內無窮階數連續可導的函式。...... 若一元函式在閉區間上分段連續,至多除有限個點之外可微且導數連續,在這有限個點存...
過分函式調和函式 編輯 稱定義在R的開集U上的復值函式f是調和的,如果它在U上二次連續可微,且它經拉普拉斯運算元作用後為零:Δf=0。...
正定函式是一個在許多領域都會遇到並且很有用的概念。如機率論中隨機變數的特徵函式就是正定函式。特徵函式比隨機變數的分布函式更易於處理。在Lyapunov穩定性理論中,...
在數學中,弱微分是一個函式的微分(強微分)概念的推廣,它可以作用於那些勒貝格可積(Lebesgue Integrable)的函式,而不必預設函式的可微性(事實上大部分可以弱微分的...
微分學,是指研究函式的導數與微分及其在函式研究中的套用。微分學與積分學聯繫密切,共同組成分析學的一個基本分支──微積分學。...
1897年大學畢業後,勒貝格在該校圖書館工作了兩年.在這期間,出版了E.波萊爾(Borel)關於點集測度的新方法的《函式論講義》(Lecons sur la théorie des functions ...
