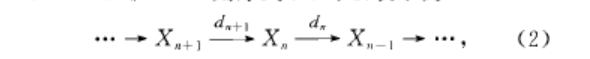
上復形亦稱上鏈一種特殊的模同態序列.設有A一同態序列
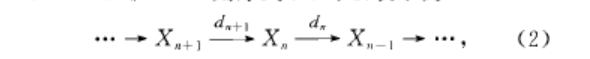
上復形亦稱上鏈一種特殊的模同態序列.設有A一同態序列上復形(cocomplex)亦稱上鏈一種特殊的模同態序列.設有A一同態序列這個序列的兩個方向都是無限的，若對每個整數n皆有d"+' d" - 0，則稱序列(1)為環A上...
鏈復形(chain complex)是一種抽象的復形。復形常指上復形。上復形亦稱上鏈。一種特殊的模同態序列。類似地可定義和討論與鏈復形有關的鏈映射、鏈同倫以及鏈復形的同調序列等同調理論。從單純同調群和奇異同調群的理論可看出這些對象有許多共同特徵。簡介 鏈復形(chain complex)是一種抽象的復形。定義 設{C}...
上鏈復形（cochain complex）是1993年公布的數學名詞。定義 上鏈復形 為分次左Λ模範疇 的對象，並配有次數為1的冪零自同態 ，其中 稱為微分或上邊緣運算元。與鏈復形的關係 上鏈復形與鏈復形的差別是形式上的而不是實質性的。設 是上鏈復形，把 寫成 ,把 寫成 就得到一個鏈復形 .反之亦然，只需要把...
那么稱K為單純復形，簡稱復形。K中單形維數的最大值為K的維數，記作 ，K的零維單形稱為K的頂點。單純復形的連通性 單純復形的連通性(connectivity of simplicial complex)是拓撲空間的連通性在復形上的推廣。若復形K不是兩個非空不相交的子復形的並集，則稱復形K是連通的。若L是復形K的連通子復形，...
模上復形 模上復形（complex over a module）是1993年公布的數學名詞。公布時間 1993年，經全國科學技術名詞審定委員會審定發布。出處 《數學名詞》第一版。
CW復形是由一些（有限多個或無窮多個）胞腔從低維到高維逐層堆積而成的空間。簡介 CW復形是劃分為各維胞腔的豪斯多夫空間。定義 設X為豪斯多夫空間。則CW復形為X與其閉子空間上升列X⁰⊂X¹⊂X²⊂...，滿足 (1)X⁰定義了離散拓撲。(2)X為j:Sⁿ→Xⁿ與Sⁿ↪D的推出。(3)X=⋃...
抽象復形是幾何復形的一種抽象。將幾何單純復形的一些良好性質，利用同構復形的思想，加以抽象化就得到抽象復形的概念，同構的復形對應同一個抽象復形。簡介 抽象復形是單純復形的一種抽象化。定義 抽象復形K由一個非空集合A（稱為頂點集），與A的非空有限子集族𝓚（𝓚中元稱為單形）構成，並滿足條件：...
雙復形(bicomplex)亦稱二重複形.復形概念的推廣.它是上雙復形的對偶概念.設M=Mh9pyEZ是雙分次模，a[一1,0];M->M與0，一1M->M是分次模映射。雙復形(bicomplex)亦稱二重複形.復形概念的推廣.它是上雙復形的對偶概念.設M=Mh9pyEZ是雙分次模，a[一1,0];M-＞M與0，一1M-＞M是分次模映射，...
三復形 三復形是雙復形概念的推廣.設M= {Mp4> } p,q,rE Z}是三分次模。三復形，雙復形概念的推廣.設M= {Mp4> } p,q,rE Z}是三分次模，是分次模映射，並且dd=O,aa=O,}}=O,ad=da,a}=}a, }d=d}
復形範疇 復形範疇是一種特殊的範疇。定義 設 為加性範疇，範疇 的對象為 的復形、態射為 的復形之間的態射，則 為復形範疇。性質 為 的全子範疇。
環繞復形(linked complex)是一類特殊的復形.為刻畫復形的多面體在一點附近的性質引進的局部同調群，需要引人環繞復形概念。環繞復形，一類特殊的復形.為刻畫復形的多面體在一點附近的性質引進的局部同調群，需要引人環繞復形概念.設K是復形，對於任意點二E IKI，二點的單純鄰域N LK(x)={t E N(二)}二告t...
單純復形（Simplicial Complex）是拓撲學中的概念，指由點、線段、三角形等單純形“粘合”而得的拓撲對象。單純復形不應當與範疇同倫論中的單純集合混淆。單純復形亦稱幾何單純復形。單純同調論中的一個基本概念。用單形構造的並且按一定規則組成的圖形。它是定義一類拓撲空間的工具。拓撲學中的定義 數學中，單純復...
同構復形(isomorphic complexes)本質上沒有差別的兩個復形.設K和L是兩個復形。若K的全體頂點集K。一{a;li一0,1,2,}}},r}和L的全體頂點集L0= {bai=0,1,... }l}之間存在一個一一對應(因而K和1的頂點個數相同，設是r+1個)，中:K0~L0，a; I--} b; (i一0，1，2，…,r)，使得((a;0...
上同調模(cohomology modules)是一種重要的模。指由上復形給出的模。設：是環A上的復形，因為 dd=0，所以 ，於是 為A模，稱此模為上復形X的上同調模。分別以 來表示 ，把 的元素分別稱為上鏈、上循環、上邊緣、上同調類。若X是環A上的復形，則對偶地可以定義復形X的同調模Hₙ(X)=ker dₙ/Im...
一個結合代數的形變跟它的Hochschild上復形有密切的關係，Gerstenhaber證明，Hochschild上復形實際上形成一個微分分次李代數，並且這個微分分次李代數完全控制了該結合代數的形變。Gerstenhaber的研究受到小平邦彥(Kodaira)-Spencer關於流形復結構形變研究的啟發，這些思想後來由Deligne和Kontsevich等人加以系統完成。在上面後...
研究結果如下： 1. 在申請人和Alexander Polishchuk的合作工作中，我們構造了d維Calabi-Yau流形上復形模空間上的shifted Poisson結構。 2. 作為一個特殊的例子，3維Sklyanin代數的希爾伯特概型對應 d=1情形的一類長度為3的復形的模空間。我們的結果給出了Nevins-Stafford結果一個不同的證明。 3. 在d=1的情形，...
跰趾，又稱“復甲”“跰甲”，在醫學上稱作瓣狀（petaloidtoenails，PTN）或小腳趾復形，是指小腳趾甲分瓣而非完整一塊。西方醫學認為，這是一種腳部的病變，是一種由摩擦生成的繭子。稱為Lister's corn。實際上瓣狀甲是一個常染色體顯性性狀，不能作為一個族群的特定標誌。傳說 在距今640多年前的明洪武年間，...
