三復形是雙復形概念的推廣.設M= {Mp4> } p,q,rE Z}是三分次模。
基本介紹
- 中文名:三復形
- 外文名:tricomplex
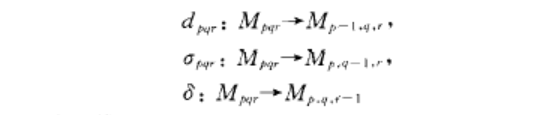

三復形是雙復形概念的推廣.設M= {Mp4> } p,q,rE Z}是三分次模。
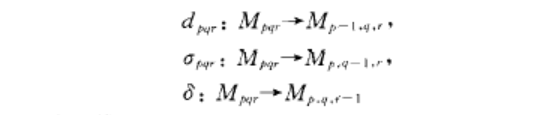
三復形是雙復形概念的推廣.設M= {Mp4> } p,q,rE Z}是三分次模。三復形,雙復形概念的推廣.設M= {Mp4> } p,q,rE Z}是三分次模,是分次模映射,並且dd=O,aa=O,}}=O,...
分別是PP和Q。的恆等映射,則(M,d',d'')是一個雙復形,其復形Tot將表以屍⑧。Q或p⑧Q,稱之為復形P與Q的張量積.周伯塤於1982年定義了三復形的全復形,在三復形上從一些模的投射分解與內射分解,來研究全復形的同調模,並求出與函子Tor的一些關係.同時,把雙復形上的孔乃特定理推廣到三復形上.
積復形 積復形(product complex)是1993年公布的數學名詞。公布時間 1993年,經全國科學技術名詞審定委員會審定發布。出處 《數學名詞》第一版。
單純復形(Simplicial Complex)是拓撲學中的概念,指由點、線段、三角形等單純形“粘合”而得的拓撲對象。單純復形不應當與範疇同倫論中的單純集合混淆。單純復形亦稱幾何單純復形。單純同調論中的一個基本概念。用單形構造的並且按一定規則組成的圖形。它是定義一類拓撲空間的工具。拓撲學中的定義 數學中,單純復...
CW復形是由一些(有限多個或無窮多個)胞腔從低維到高維逐層堆積而成的空間。簡介 CW復形是劃分為各維胞腔的豪斯多夫空間。定義 設X為豪斯多夫空間。則CW復形為X與其閉子空間上升列X⁰⊂X¹⊂X²⊂...,滿足 (1)X⁰定義了離散拓撲。(2)X為j:Sⁿ→Xⁿ與Sⁿ↪D的推出。(3)X=⋃...
復形的多面體,亦稱復形的基礎空間一類特殊的拓撲空間.復形是代數拓撲中的基本概念,以它作為工具進行研究,而最終目的是得出它所給出的拓撲空間,也就是多面體的拓撲性質.若K是n維歐氏空間R"中的復形,則K中全體單形的所有點組成的集合作為R"的子空間稱為K的多面體,記為}K},K稱為多面體}KI的一個單純剖分或...
是一一對應.對於不同維的映射,這些條件不一定成立,惠特尼在1936年給出過2維復形到2維或3維射影空間的映射同倫的代數條件,但未發表.1941年,H.E.羅賓斯(Robbins)推廣到2維復形到任何空間的映射的同倫分類,後來P.奧蘭姆(Olum)又大規模地予以簡化及推廣.對3維復形,龐特里亞金在1941年考慮它到S2的映射...
傘形花序是無限花序的一種。其特點是花軸縮短,大多數花著生在花軸頂端,每朵小花的花柄基本等長,因而小花在花軸頂編排列成圓頂形,開花的順序是由外向內,如蔥、人參等。復傘形花序:傘形花序的每一傘梗再生出一個傘形花序,即二回傘形花序,以此類推有三回乃至多回傘形花序。凡此都稱做復傘形花序。圖冊參考...
無窮遠點的算數有時和一般的代數規則不符,因此擴充複數不構成一個代數域。但是,黎曼球面在幾何和解析角度都行為良好,甚至在無窮遠點也不例外;它是一個一維復流形,也稱黎曼曲面。複分析中,黎曼球面對於亞純函式這個優雅的理論很有幫助。黎曼球面在射影幾何和代數幾何中作為複流形、射影空間和代數簇的基本例子...
單形名稱晶面數目單形單獨存在時晶面的形狀橫切面形狀*所屬晶系四方雙錐(正方雙錐)8等腰三角形正方形復四方雙錐(復正方雙錐)16不等邊三角形復四方形四方晶系三方雙錐6等腰三角形等邊三角形三方、六方晶系復三方雙錐12不等邊三角形復三方形六方晶系六方雙錐12等腰三角形正六邊形三方、六方晶系復六方雙錐24不等...
11.3 四元數幾何 11.4 轉動如何疊加 11.5 克利福德工數 11.6 格拉斯曼代數 第十二章 n維流形 12.1 為什麼要研究高維流形?12.2 流形與坐標拼塊 12.3 標題、矢量和余矢量 12.4 格拉斯曼積 12.5 形式的積分 12.6 外導數 12.7 體積元,求和規則 12.8 張量:抽象指標記法和圖示記法 12.9 複流形 ...
