一階偏微分方程是最簡單的一類偏微分方程。一階偏微分方程的幾何理論有悠久的歷史淵源,以後經過É.(-J.)嘉當等人的發展,在幾何學、力學和物理學中都有重大的意義。
基本介紹
- 中文名:一階偏微分方程
- 外文名:partial differential equation of first order
- 實質:微分
- 特點:最簡單的偏微分
- 詞條類型:數學
定義
偏微分方程
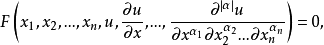


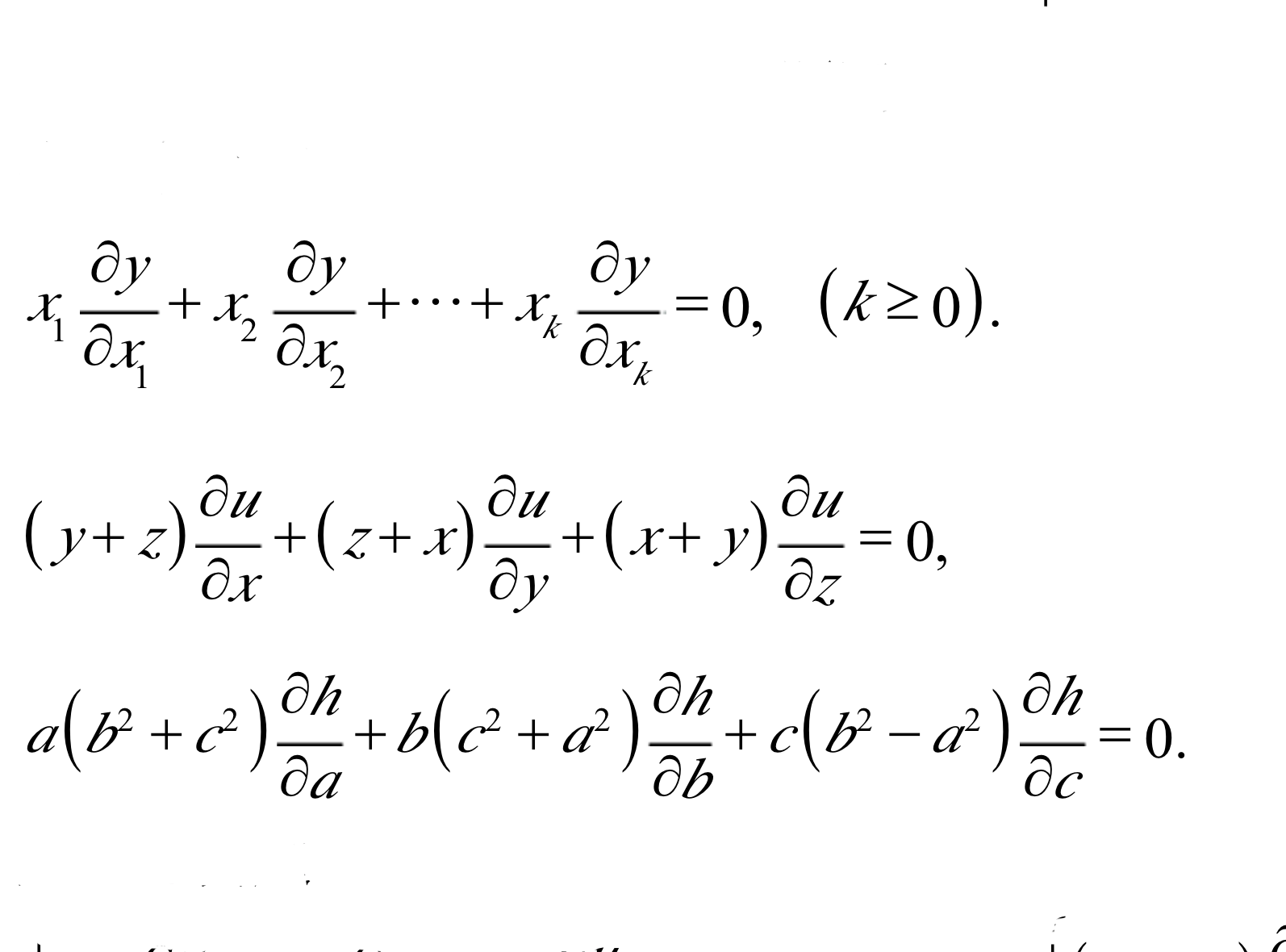
一階偏微分方程是最簡單的一類偏微分方程。一階偏微分方程的幾何理論有悠久的歷史淵源,以後經過É.(-J.)嘉當等人的發展,在幾何學、力學和物理學中都有重大的意義。
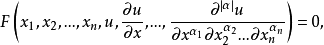


一階偏微分方程是最簡單的一類偏微分方程。一階偏微分方程的幾何理論有悠久的歷史淵源,以後經過É.(-J.)嘉當等人的發展,在幾何學、力學和物理學中都有重大的...
形如y'+P(x)y=Q(x)的微分方程稱為一階線性微分方程,Q(x)稱為自由項。一階,指的是方程中關於Y的導數是一階導數。線性,指的是方程簡化後的每一項關於y...
一階擬線性偏微分方程(quasi-linear partial differential equation of first order)是一類特殊的一階非線性偏微分方程,關於未知函式的偏導數是線性的一階非線性偏...
包含未知函式的偏導數(或偏微分)的方程。方程中所出現未知函式偏導數的最高階數,稱為該方程的階。在數學、物理及工程技術中套用最廣泛的,是二階偏微分方程,習慣...
微分方程指含有未知函式及其導數的關係式。解微分方程就是找出未知函式。微分方程是伴隨著微積分學一起發展起來的。微積分學的奠基人Newton和Leibniz的著作中都處理過...
一階非線性偏微分方程(non-linear partial dif- ferential equation of first order)一階的完全非線 J勝偏微分方程.兩個自變數的一階非線性偏微分方 程的一般...
形如y'=f(y/x)的一階微分方程,稱為齊次一階微分方程。齊次微分方程是一個微分方程,如果它的一個解乘以任意常數後,仍是它的解,則稱為齊次微分方程。對一階...
偏微分方程特徵理論是偏微分方程論的一個基本概念。它對研究解的存在、唯一性及其他性質(例如奇性傳播)都有重要的意義。...
《高等院校重點課程教材:偏微分方程》主要介紹波動方程、熱傳導方程和位勢方程定解問題的推導及其求解方法,還對兩個自變數的一階偏微分方程組作了簡單介紹。全書共...
凡是可用一階微分方程描述的系統稱一階系統。...... 一階系統編輯 鎖定 本詞條由“科普中國”百科科學詞條編寫與套用工作項目 審核。凡是可用一階微分方程描述的系...
《基礎偏微分方程》是2006年6月1日高等教育出版社出版的圖書。作者是布利克、科達斯。本書是數學翻譯叢書中的一本,是基於作者多年教學經驗的積累而編寫的一本起點...
定義2:任何代入微分方程後使其成為恆等式的函式,都叫做該方程的解.若微分方程的解中含有任意常數的個數與方程的階數相同,且任意常數之間不能合併,則稱此解為該...
微分方程大致與微積分同時產生 。事實上,求y′=f(x)的原函式問題便是最簡單的微分方程。而如果在該方程中y連續求兩次導數的話就是二階微分方程。...
《偏微分方程基本理論》是2009年科學出版社出版的圖書,作者是王明新。...... 理論》系統介紹了二階線性橢圓型方程、拋物型方程和雙曲型方程以及一階偏微分方程的基...
《線性偏微分方程講義》是2011年哈爾濱工業大學出版社出版的圖書,作者是L·尼倫伯格。...
簡單來講,線性微分方程是指關於未知函式及其各階導數都是一次方,否則稱其為非線性微分方程。...
《偏微分方程》是2010年高等教育出版社出版的圖書,作者是孔德興。...... 《偏微分方程》共分八章:第一章為緒論;第二、三章分別介紹了一階方程、具有兩個自變數...
