衰變模型
α-decay
性質
設衰變前的
原子核(稱母核)為X(
Z,
A),這裡
Z為
原子序數,
A為
質量數,衰變後的原子核(稱
子核)為Y(
Z-2,
A-4),則α衰變可表示為
X(Z,A)→Y(Z-2,A-4)+α
α衰變能Qα可表示為
Qα=(mx-my-mα)c2,
其中
mx、
my和
mα分別是母核、子核和α 粒子的
靜止質量,с是真空中的
光速。
Qα=Eα+Ey,
可見,對
A≈200的
原子核,α粒子的動能約占衰變能的98%,子核的反衝能約占衰變能的2%。實驗測得α粒子的動能因母核而異,一般在4~9兆電子伏之間。因而子核反衝能約為 100千電子伏量級。這個能量足以引起一些重要的反衝效應。
絕大多數的α放射體放出的α粒子的能量不止一組,而有強度不等的若干組,這是由於α衰變不僅在母核
基態至子核基態之間進行,而且可以在母核基態至子核激發態之間,少數情形可以在母核激發態至子核基態之間進行。
在天然
核素中,只有相當重的核(
A> 140的核)才可能發生α衰變,而且主要發生於
A> 209的重核。利用核子的
平均結合能不難解釋這一現象(見
原子核)。
不同的α放射性核素具有不同的
半衰期,半衰期的長短同α粒子的能量有強烈的依賴關係。例如U238放射的α粒子能量是4.20兆電子伏,而Po212放射的α粒子能量是8.78兆電子伏,相差2.1倍,而U238的半衰期是4.468×10^9年,而Po212的半衰期是3.0×10^-7秒,卻相差10^23倍。這反映了α粒子能量的微小改變引起了半衰期的巨大變化。1911年,H.蓋革和J.M.努塔耳總結實驗結果,得出
衰變常數λ和α粒子能量之間的經驗規律。這個規律可以表述為
lgλ=A+BlgEα,
衰變常數λ同半衰期
T12的關係是:
T12 = ln2/λ,而
B是常數(約86),
A對同一個天然
放射系也是常數。
產生機制
為什麼α粒子能從
原子核中發射出來,為什麼α衰變具有一定半衰期,為什麼半衰期同α粒子能量有強烈的依賴關係,這些都是人們十分感興趣的問題。計算表明,α粒子和
子核之間的
庫侖勢壘一般高達20兆電子伏以上。如前所述,α粒子動能比庫侖勢壘高度低得多,按照
經典力學,由於庫侖勢壘的阻擋,α粒子不能跑到核外,根本不可能發生α衰變。20世紀20年代發展起來的
量子力學能成功地解釋 α衰變的產生機制。根據量子力學的
隧道效應,α粒子有一定的幾率穿透
勢壘跑出原子核。描述勢壘穿透幾率
P的
伽莫夫公式是
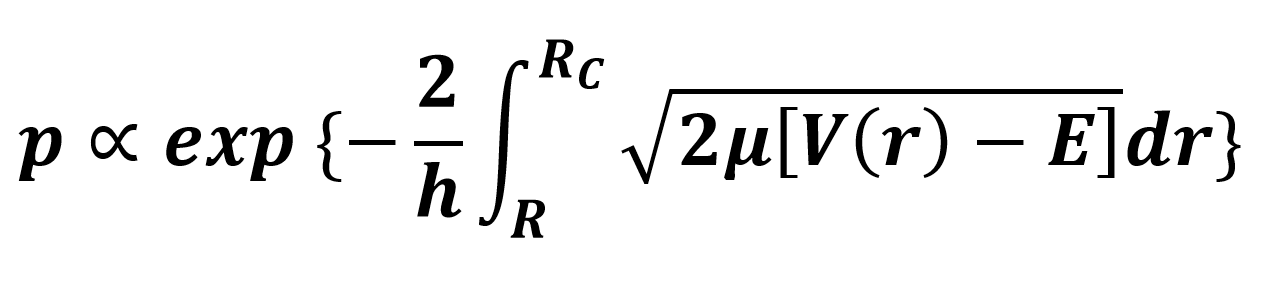 伽莫夫公式
伽莫夫公式式中
V(r)是α粒子和
子核的相互作用勢,
E是相對運動動能,
μ是α粒子和子核的
約化質量,
Rc是α粒子與子核的半徑之和,
R是
V(r)=
E時的r值。可見,α粒子的能量
E越大,穿透勢壘的幾率就越大,衰變幾率就越大,從而半衰期就越短。由於能量因子出現在
伽莫夫公式的指數冪上,因而它的微小變化將引起
衰變常數的巨大變化。這就解釋了實驗上觀察到的α衰變半衰期隨α粒子能量變化而劇烈變化的規律。利用勢壘穿透來解釋 α衰變是用
量子力學研究
原子核的最早成就之一。
半衰期
不同
核素α衰變的半衰期分布較廣,從1微秒(μs)到1017秒(s),一般的規律是衰變能較大,則半衰期較短;反之,衰變能較小,則半衰期較長。衰變能的微小改變,引起半衰期的巨大變化。α衰變是
量子力學隧道效應的結果,半衰期隨衰變能變化的規律可以根據隧道效應予以說明。計算表明,α粒子和
子核的
庫侖勢壘高達20MeV,α粒子的能量雖小於此值,但由於隧道效應,α粒子有一定的幾率穿透勢壘,跑出
原子核。α粒子的能量越大,穿透勢壘的幾率越大,即衰變幾率越大,從而半衰期越短。由於能量因子出現在指數上,因而它的微小變化,引起半衰期的巨大變化。這是量子力學研究原子核的最早成就之一。
α衰變主要限於一些
重核素。α衰變
能譜的研究提供了核結構的信息。α
衰變常數的定量計算直到目前還沒有得到圓滿解決。尤其對於奇
A核和奇奇核,實驗值可以比理論值小几個
數量級。這主要有賴於所謂 α形成因子的計算。研究表明:α粒子不大可能在α衰變前就存在於核內,而是在衰變過程中形成的。因此,在計算衰變常數時,必須乘上一個有關
α粒子形成幾率的因子,通常稱它為α形成因子。顯然,α形成因子應該和
原子核的結構有關。正因為如此,對α衰變的深入研究可進一步了解原子核內部結構的運動規律。
參考書目
P.Marmier and E.Sheldon,Physics of Nuclei and Particles,Academic Press,New York and London,1969.

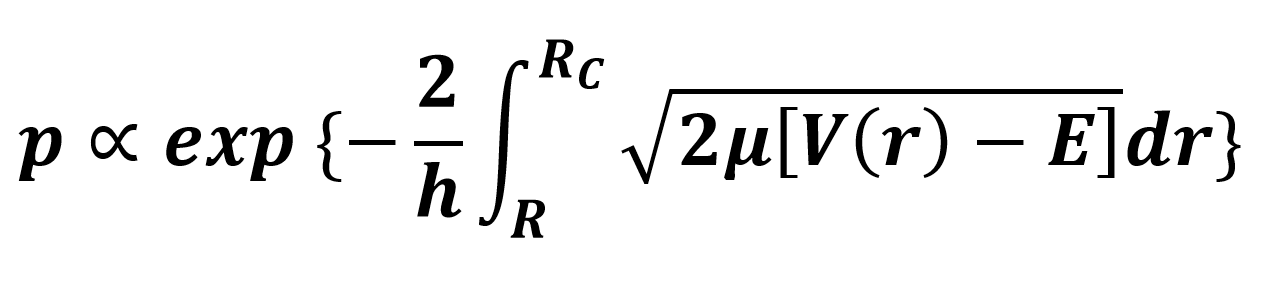 伽莫夫公式
伽莫夫公式
