介紹 β衰變
β-decay
β衰變的
半衰期 分布在接近10秒到10年的範圍內,發射出粒子的能量最大為幾兆電子伏。β衰變不僅在重核範圍內發生,在全部
元素周期表 範圍內都存在β
放射性 核素。因此,對β衰變的研究比
α衰變 的研究更重要。
X→ Y+e- +-ve(β- 衰變)
X→ Y+e+ +ve(β+ 衰變)
X+e- → Y+ve(EC)
式中X和Y分別代表母核和子核;A和Z是母核質量數和電荷數;
三種類型釋放的衰變能分別為
Qβ-=(mx-mY)c^2
Qβ+=(mx-mY-2me)c^2,
QEC=(mx-mY)c^2-wi
式中mX、mY分別為母核原子和子核原子的靜質量;me為電子靜質量;wi為軌道電子結合能;c為
真空 光速。
軌道電子俘獲 可俘獲K層電子 ,稱為K俘獲 ;也可以俘獲L層電子,稱為L俘獲。軌道電子俘獲所形成的
子核 原子於缺少一個內層電子而處於
激發態 ,可通過外層
電子躍遷 發射X
射線 標識譜 或發射
俄歇電子 而退激。最初以為β-連衰變僅放出電子,實際測量發現,放出的電子能 量從零到 Qβ- 連續分布 ,曾困惑物理學家多年 。
1930年W.E.
泡利 提出β-衰變放出e-的同時還放出一個靜質量為零、
自旋 為1/2的
中性粒子 ,衰變能為電子和該粒子分享 ,該粒子後來被稱為
中微子 ,1952年以後被實驗確鑿證實。
β衰變屬於
弱相互作用 。1956 年李政道和楊振寧提出弱相互作用過程
宇稱 不守恆,第二年
吳健雄 等人利用極化核
60 Co的β衰變實驗首次證實了宇稱不守恆 。這一發現不僅促進了β衰變本身的研究,也促進了粒子物理的發展。
發展 β衰變 是
放射性 原子核 放射電子(
β粒子 )和
中微子 而轉變為另一種核的過程。1896年,亨利·貝克勒(A. H. Becquerel)發現
鈾 的放射性;1897年,
盧瑟福 (E. Rutherford)和
約瑟夫·湯姆孫 (J. J. Thomson)通過在磁場中研究鈾的放
射線 偏轉,發現鈾的放射線有帶
正電 ,帶負電和不帶電三種,分別被稱為
α射線 ,
β射線 和
γ射線 ,相應的發出β射線衰變過程也就被命名為β衰變。
放出正電子的稱為“正β衰變”,放出電子的稱為“負β衰變”。在正β衰變中,核內的一個
質子 轉變成中子,同時釋放一個正電子和一個中微子;在負β衰變中,核內的一個中子轉變為質子,同時釋放一個電子和一個
反中微子 。此外
電子俘獲 也是β衰變的一種,稱為電子俘獲β衰變。
因為
β粒子 就是電子,而電子的質量比起核的質量來要小很多,所以一個
原子核 放出一個β粒子後,它的質量只略微減少。
衰變規律 新核的
質量數 不變,電荷數增加1,新核在
元素周期表 中的位置要向後移一位。β衰變中放出的電子能量是連續分布的,但對每一種衰變方式有一個最大的限度,可達幾兆
電子伏特 以上,這部分能量由
中微子 帶走。
原理 三種類型
β衰變中,原子核發生下列三種類型的變化:
其中
m x和
m y為母核
原子 和子核原子的
靜止質量 ,
m e為電子的靜止質量,
W i為軌道電子結合能,с為
光速 。
β衰變 軌道電子俘獲 過程所形成的
子核 原子,由於缺少了一個內層電子,原子處於激髮狀態,它可以通過不同方式退激。對於K俘獲,當L層電子跳到K層填充空位,可以發射標識X
射線 ,或稱特徵X 射線。它的能量是 K層和L層電子的
結合能 之差
hv =
W k-
W L;當L層電子跳到K層空位時,也可以不發射標識X射線,而把能量交給另一個L層電子,使其克服結合能而飛出,這種電子稱為
俄歇電子 ,它的動能
E e=
hv -
W L=
W k-2
W L。軌道電子俘獲總伴隨有標識X射線或俄歇電子的產生。
β衰變的電子
中微子 理論 β衰變中放出的
β粒子 的能量是從 連續分布的。為了解釋這一現象,1930年,W.泡利提出了β衰變放出中性微粒的假說。1933年,E.費密在此基礎上提出了β衰變的電子中微子理論。這個理論認為:
中子 和
質子 可以看作是同一種粒子(
核子 )的兩個不同的量子狀態,它們之間的相互轉變,相當於核子從一個
量子態 躍遷到另一個量子態,在躍遷過程中放出電子和中微子。β粒子是核子的不同狀態之間躍遷的產物,事先並不存在於核內。所以,引起β衰變的是電子-中微子場同
原子核 的相互作用,這種作用屬於
弱相互作用 。這個理論成功地解釋了β譜的形狀,給出了β衰變的定量的描述。
β躍遷幾率 根據量子力學的微擾論,費密理論給出單位時間發射動量在
p 到
p +d
p 間
β粒子 的幾率為, (1)
β衰變 β躍遷分類 根據躍遷矩陣元的大小,可將β躍遷分為容許躍遷、一級禁戒躍遷、二級禁戒躍遷等。級次越高,躍遷幾率越小;相鄰兩級間,幾率可以相差幾個數量級。
費密理論給出β衰變對母核同子核間的
自旋 和
宇稱 變化的選擇定則:對於允許躍遷,自旋變化|Δ
I |=0,1,宇稱變化 Δ
π =+1;對於一級
禁戒躍遷 ,|Δ
I |=0,1,2,Δ
π =-1;對於二級以上的如
n 級禁戒躍遷,|Δ
I |=
n ,
n +1,Δ
π =(-1)。
β衰變的居里描繪
在β衰變的研究中,常將式(1)改寫為, (2)式中。對
容許躍遷 ,|
M if|與
β粒子 的能量無關,
K 為常數。此時若以為縱坐標,
E 為橫坐標作圖,則得一條直線。直線同橫軸的交點為β粒子的最大能量
E m。這種圖稱為居里描繪,也稱費密-居里圖。這樣,居里描繪可用來精確地測定
E m。此外,也可用來分解複雜的β譜。對於
禁戒躍遷 ,
M if往往不是常數,則按式(2)作圖時不是一條直線。這時可引入一個同β粒子能量有關的因子
S n(
E )對居里描繪進行改正,即把
K 中同能量有關的因子分出來,,使
K ┡為常數。此時式(2)可寫成
β衰變 ,改正後的居里描繪取
β衰變 對
E 作圖,仍是一條直線。
S n(
E )由理論可以計算。因而,通過理論同實驗的比較,可決定
S n(
E ),從而可以定出
禁戒躍遷 級次
n 。
β衰變 薩晉關係
通過對
β粒子 動量分散式(1)的積分,假定躍遷
矩陣 元
M if同β粒子能量的關係可以忽略,便得到β
衰變常數 λ或半衰期
T ½。,(3)
β衰變 式中f (Z ,E m)稱為費密積分函式。p m為電子的最大動量。
當β粒子的最大能量遠大於它的靜止能量,並且可以忽略核的庫侖場對發射β粒子的影響時,
β衰變 從而可得關係。
由薩晉關係可見,僅僅以半衰期(或衰變常數)的大小不能反映β躍遷的級次。
因此需要引入比較半衰期
fT ½。由於
fT ½值與|
M if|成反比,而|
M if|的大小對不同級次的躍遷有很大差別,從而
fT ½值可用來比較躍遷的
β衰變 級次。這就是稱fT ½為比較半衰期的由來。
實驗測得的各級躍遷的lgfT ½值大致範圍如下:躍遷級次 lgfT ½
容 許 3~6一級禁戒 6~10二級禁戒 10~13
β衰變 三級禁戒 15~18β
衰變中的宇稱不守恆
在β衰變的研究中的一個重要的突破是1956年
李政道 和
楊振寧 提出的
弱相互作用 中的宇稱不守恆,第二年
吳健雄 等人利用極化核鈷的β衰變實驗首次證實了宇稱不守恆,這一發現不僅促進了β衰變本身的研究,也促進了
粒子物理學 的發展。
雙重β衰變 β衰變 雙重β衰變,亦作ββ衰變,是β衰變的一個特例,包含原子核內兩個單位的轉變,只發生於特定的原子核。雙重β衰變正常來說會放出兩對中微子,但現時有科學家猜想是否有可能發現不放出中微子的雙重β衰變,稱為“無中微子雙β衰變”。物理學者尚未能驗證此程式存在,推長
半衰期 下限至10年。
 β衰變
β衰變 β衰變
β衰變 β衰變
β衰變 β衰變
β衰變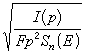 β衰變
β衰變 β衰變
β衰變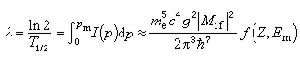 β衰變
β衰變
 β衰變
β衰變 β衰變
β衰變 β衰變
β衰變 β衰變
β衰變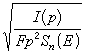 β衰變
β衰變 β衰變
β衰變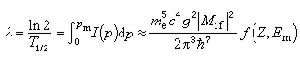 β衰變
β衰變