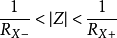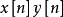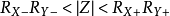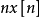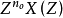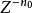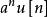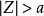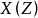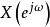簡介
Z變換(Z-transform) 將離散系統的時域數學模型——差分方程轉化為較簡單的頻域數學模型——代數方程,以簡化求解過程的一種數學工具。離散信號系統的系統函式(或者、稱傳遞函式)一般均以該系統對單位抽樣信號的回響的Z變換表示。由此可見,Z變換在離散系統中的地位與作用,類似於連續系統中的拉氏變換。
Z變換具有許多重要的特性:如線性、時移性、微分性、序列卷積特性和復卷積定理等等。這些性質在解決信號處理問題時都具有重要的作用。其中最具有典型意義的是卷積特性。由於信號處理的任務是將輸入信號序列經過某個(或一系列各種)系統的處理後輸出所需要的信號序列,因此,首要的問題是如何由輸入信號和所使用的系統的特性求得輸出信號。通過理論分析可知,若直接在時域中求解,則由於輸出信號序列等於輸入信號序列與所用系統的單位抽樣回響序列的卷積和,故為求輸出信號,必須進行繁瑣的求卷積和的運算。而利用Z變換的卷積特性則可將這一過程大大簡化。只要先分別求出輸入信號序列及系統的單位抽樣回響序列的Z變換,然後再求出二者乘積的反變換即可得到輸出信號序列。這裡的反變換即逆Z變換,是由信號序列的Z變換反回去求原信號序列的變換方式。
當前,已有現成的與拉氏變換表類似的Z表。對於一般的信號序列,均可以由表上直接查出其Z變換。相應地,當然也可由信號序列的Z變換查出原信號序列,從而使求取信號序列的Z變換較為簡便易行。
歷史
Z變換的基本思想眾所周知來自
拉普拉斯。在1947年由W. Hurewicz重新引入作為一個易操縱的方式來解決線性常係數差分方程。它後來於1952年在哥倫比亞大學被Ragazzini和Zadeh冠以“the z-transform“用於採樣。
雙邊Z變換
離散時間序列x[n]的Z變換定義為:
式中
,σ為實變數,ω為實變數,所以Z是一個幅度為
,相位為ω的復變數。x[n]和X(Z)構成一個Z變換對。
單邊Z變換
通常意義下的Z變換指雙邊Z變換,單邊Z變換隻對右邊序列(
部分)進行Z變換。單邊Z變換可以看成是雙邊Z變換的一種特例,對於因果序列雙邊Z變換與單邊Z變換相同。
收斂域
Z變換的存在
充分必要條件是:級數絕對可和。使級數絕對可和的成立的所有Z值稱為Z變換域的收斂域。由Z變換的表達式及其對應的收斂域才能確定原始的離散序列。收斂域可用公式表示為:
特點
(1)收斂域是一個圓環,有時可向內收縮到原點,有時可向外擴展到∞,只有
的收斂域是整個Z平面;
(2)在收斂域內沒有極點,X(Z)在收斂域內每一點上都是解析函式。
分類
(1)有限長序列
顯然|Z|在整個開域
都能滿足Z變換存在條件,因此有限長序列的收斂域是除0及∞兩個點(對應n>0和n<0不收斂)以外的整個Z平面:
。如果對n
1,n
2加以一定的限制,如
或
,則根據條件
,收斂域可進一步擴大為包括0點或∞點的半開域。
 右邊序列收斂域
右邊序列收斂域(2)右邊序列
指序列
只在
有值,而
時,
,這時 ,其收斂域為收斂半徑
以外的Z平面,即
。
右邊序列Z變換可表示為:
 左邊序列收斂域
左邊序列收斂域(3)左邊序列
指序列
只在
有值,而
時,
,這時,其收斂域為收斂半徑
以內的Z平面,即
。
左邊序列Z變換可表示為:
(4)雙邊序列
可看作一個左邊序列和一個右邊序列之和,因此雙邊序列Z變換的收斂域是這兩個序列Z變換收斂域的公共部分。
雙邊序列Z變換可表示為:
(如果
,則存在公共的收斂區間,
有收斂域:
如果
,無公共收斂區間,
無收斂域,不收斂。)
 雙邊序列收斂域
雙邊序列收斂域性質
Z變換有線性性、序列移位、時域
卷積、頻移、頻域微分等性質。這些性質對於解決實際問題非常有用。其性質均可由正反Z變換的定義式直接推導得到。
| 序列 | Z變換 | 收斂域 | 備註 |
|---|
| 1 | | | | |
|---|
| 2 | | | | |
|---|
| 3 | | | | 線性性 |
|---|
| 4 | | | | 時域反轉 |
|---|
| 5 | | | | 序列卷積 |
|---|
| 6 | | | | 序列相乘 |
|---|
| 7 | | | | 序列共軛 |
|---|
| 8 | | | | 頻域微分 |
|---|
| 9 | | | | 序列移位 |
|---|
| 10 | | | | 初值定理 |
|---|
| 11 | | | | 終值定理 |
|---|
常用變換對
| 信號x[n] | Z變換X(Z) | 收斂域 |
|---|
| 1 | | 1 | 所有Z |
|---|
| 2 | | | |
|---|
| 3 | | | |
|---|
| 4 | | | |
|---|
| 5 | | | |
|---|
| 6 | | | |
|---|
| 7 | | | |
|---|
逆變換
已知Z變換X(Z)求對應的離散時間序列x[n]稱為Z變換的逆變換。逆Z變換的定義式為:
逆Z變換是一個對Z進行的圍線積分,積分路徑C是一條在
收斂環域(Rx-,Rx+)以內逆時針方向繞原點一周的單圍線。
求解逆Z變換的常用方法有:
如果得到的Z變換是冪級數形式的,則可以看出,序列值x[n]是冪級數中
項的係數;如果已經給出X(Z)的函式表達式,常常可以推導它的冪級數展開式或者利用已知的冪級數展開式,進一步X(Z)是部分分式,可用
長除法可獲得冪級數展開式。
(2)留數定律法
對於有理的Z變換,圍線積分通常可用
留數定律計算,
,即為
在圍線C內所有極點
上留數值的總和。
(3)利用已知變換對
(4)長除法
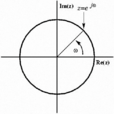
與傅立葉變換的關係
Z變換是傅立葉變換的推廣,當傅立葉變換不存在時,Z變換所定義的冪級數可能收斂。傅立葉變換是在單位圓上的Z變換,也就相當於在概念上把線性頻率軸纏繞在單位圓上,因此傅立葉變換在頻率上的固有周期性就自然得到了。
Z變換公式中,令
,可以得到離散序列的傅立葉變換與Z變換的關係:
再根據z反變換,將積分圍線取在單位圓上,得:
若具有重極點,則要將單位圓周上具有重極點的 ZT 分解成單位圓周上含極點和不含極點兩部分之和。針對單位圓周上含極點的 ZT 部分,分區內極點和區外極點兩種情況進行研究,將序列的 DTFT 分解成解析部分與不解析部分之和,對其不解析部分進行了詳細討論。








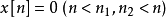
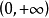




 右邊序列收斂域
右邊序列收斂域






 左邊序列收斂域
左邊序列收斂域







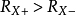




 雙邊序列收斂域
雙邊序列收斂域