基本介紹
- 中文名:統計量
- 外文名:cuscore
- 提出人:Box and Luceno
- 提出時間:1987年
研究方法,量的分析,實際運用,
研究方法
趨勢變化識別
對於一個已知分布的隨機過程,圖一. 顯示了一系列樣本函式的基本趨勢,斜率為1.0,同時一個斜率為1.3的變化(突變)移動,從時間10的地方開始出現。為了識別出樣本函式隨機變數的趨勢變化,將Cuscore統計量定義為
 圖一. 樣本函式
圖一. 樣本函式 圖二. Cuscore統計量
圖二. Cuscore統計量這種統計識別方法揭露和展示了斜率上的變化所呈現出來的證據。當斜率從初始值1.0增加30%變為1.3,其變化的幅度應該很明顯的。30%已經很接近1/3的程度,是一個很大的變化,應該引起我們的注意,但我們很難在圖一中t=10的地方識別出變化趨勢。
帶噪聲數據趨勢識別
 圖三. 隨機噪聲加入
圖三. 隨機噪聲加入量的分析
在圖四中,ABC這條線是一個趨勢變化的原型。第一個線段AB的斜率為0.5,而第二個線段BC的斜率為1.5。虛線BD是直線AB的延長線。虛線AE與直線BC平行,斜率也是1.5。當斜率發生變化,觀測值就會偏離基礎模型(也就是沒有斜率變化)的期望值。順著直線BC,y的值超過了直線BD的期望值,隨著時間地不斷增加。在圖五中,我們根據Q值的累計偏差,就可以得到如曲線1所示的圖形。
 圖四. 趨勢變化圖
圖四. 趨勢變化圖現在我們假設事先不知道直線AB與BC的斜率,也不知道在B點的斜率發生了變化。假設我們最好的理解是,從A點開始應該出現一個1.0的斜率,如直線AC所示。在圖五中,Cuscore統計量顯示為曲線2的圖形。Cuscore統計量的圖形差異極大。根據這個假設的基礎模型,得到的偏差序列,可以明顯看出趨勢的斜率發生了變化。
 圖五. β=0與β=1的Cuscore統計量
圖五. β=0與β=1的Cuscore統計量實際運用
數據監控
對自相關數據的監控,可先對數據擬合一個合適的時間序列模型,然後運用此模型來消除自相關性,對殘差進行統計過程控制 監控。 但是這些控制圖都忽略了故障表征的動態特性。因此,我們使用Cuscore統計量來進行預期信號的識別。
首先,構建如下模型
ai = ai( yi,xi,γ) i = 1,2,…,l (1)
似然函式為
l = - 1/2σ2a*Σai^2+ c
其中c 為不依賴於γ 的常數。 則有效得分統計量為

為令式(1)中γ = γ0時ai的取值,di為探測信號(detector) 。 將Cuscore 統計量定義為
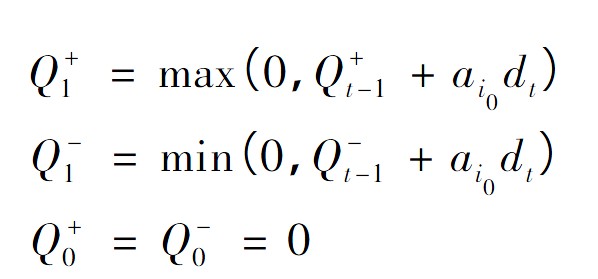
 圖六. EWMA時的Cusecore統計量
圖六. EWMA時的Cusecore統計量