移動平均值是一個最老也是最流行的技術分析工具。若依次得到一組測定值時,按順序取一定數量的數據並算得其全部算術平均值,得到的數據就叫做移動平均值。
基本介紹
- 中文名:移動平均值
- 外文名:moving average
- 性質:一種技術分析工具
- 所屬學科:數學
- 相關概念:算數平均值、移動平均法等
定義
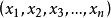
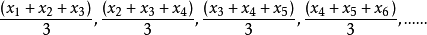
例題分析


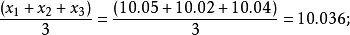

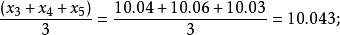

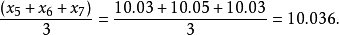
計算公式
移動平均數
一次移動平均法
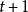
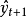

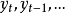
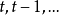
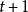

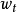



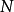
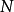
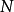
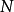
二次移動平均法




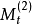



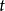
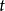
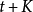
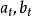
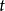
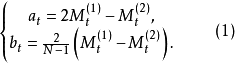

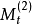



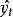


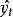

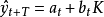
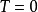
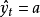

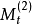



移動平均值是一個最老也是最流行的技術分析工具。若依次得到一組測定值時,按順序取一定數量的數據並算得其全部算術平均值,得到的數據就叫做移動平均值。
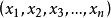
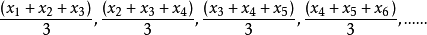


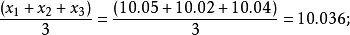

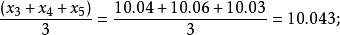

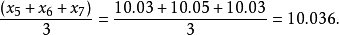
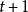
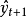

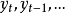
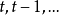
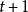

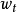



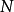
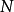
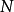
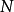




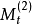



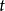
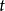
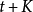
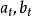
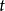
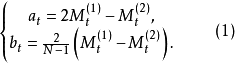

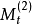



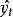


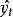

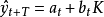
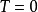
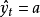

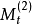


移動平均值是一個最老也是最流行的技術分析工具。若依次得到一組測定值時,按順序取一定數量的數據並算得其全部算術平均值,得到的數據就叫做移動平均值。
移動平均法是用一組最近的實際數據值來預測未來一期或幾期內公司產品的需求量、公司產能等的一種常用方法。移動平均法適用於即期預測。當產品需求既不快速增長也不...
簡單移動平均值,即算術平均值,它最常用。...... 第一種批評是,每個平均值僅僅把它所覆蓋的那段日子(例如最近10天)包括進來,第二種批評是,簡單移動平均值對其中...
移動平均數預測法是教育預測的方法。以時間序列的一組數據為基礎,推導出下一段時間數量變化的可能性。一組數據因受各種偶然因素的影響,表現不規則,偶然性很大。...
移動平均法是用一組最近的實際數據值來預測未來一期或幾期內公司產品的需求量、公司產能等的一種常用方法。移動平均法適用於近期期預測。當產品需求既不快速增長也...
EMA(Exponential Moving Average)是指數移動平均值。也叫EXPMA指標,它也是一種趨向類指標,指數移動平均值是以指數式遞減加權的移動平均。理解了MA、EMA的含義後,就...
移動平均線,Moving Average,簡稱MA,原本的意思是移動平均,由於我們將其製作成線形,所以一般稱之為移動平均線,簡稱均線。它是將某一段時間的收盤價之和除以該周期...
移動平均價是SAP系統根據移動平均法計算出的物料價格。包括在收貨及收發票中的計價過程和在生產過程中的計價過程。...
一次移動平均法是指將觀察期的數據由遠而近按一定跨越期進行一次移動平均,以最後一個移動平均值為確定預測值的依據的一種預測方法。...
移動平均控制圖是利用最近n個觀測值(其中現行觀測值已取代n+1個觀測值中的最初觀測值)的算術平均值,是評估過程水平的控制圖。移動平均控制圖可以改善在生產過程中...
移動平均季節指數,是利用移動平均法分解時間序列四類變動因子,計算出既消除長期趨勢變動又消除循環變動和不規則變動的、比較精確地反映季節變動情況的季節指數,並據此...
加權移動平均法,是對觀察值分別給予不同的權數,按不同權數求得移動平均值,並以最後的移動平均值為基礎,確定預測值的方法。採用加權移動平均法,是因為觀察期的...
複合移動平均數法是技術分析中同時使用兩種或兩種以上的移動平均數對比分析股市運動趨勢的技術方法。當短周期移動平均數曲線與較長周期的移動平均數曲線發生交叉時,...
移動平均擺動量(MAOSC)是二條不同時間周期的移動平均線的差值或比值,反映的是股價的擺動程度。移動平均擺動量指標是短線進出指標。與乖離率(BIAS)、擺動量指標(...
譯指數平滑移動平均線是因應移動平均線被視為落後指標的缺失而發展出來的,為解決一旦價格已脫離均線差值擴大,而平均線未能立即反應,EXPMA可以減少類似缺點。...
指數加權移動平均線是一種特殊的加權移動平均線。與一般的加權移動平均線一樣,指數加權移動平均線也採取前沿加重方式。...
移動平均線(MA)是以道·瓊斯的“平均成本概念”為理論基礎,採用統計學中“移動平均”的原理,將一段時期內的股票價格平均值連成曲線,用來顯示股價的歷史波動情況,...
MA,移動平均線, Moving Average,原本的意思是移動平均,由於我們將其製作成線形,所以一般稱之為移動平均線,簡稱均線。它是將某一段時間的收盤價之和除以該周期。...
“平均”是指最近n天收市價格的算術平均線;“移動”是指我們在計算中,始終採用最近n天的價格數據。因此,被平均的數組(最近n天的收市價格)隨著新的交易日的更迭...
加權移動平均線加權移動平均線 (WMA) ,它比重以平均線的長度設定,愈近期的收市價,對市況影響愈重要。計算方式是基於加權移動平均線日數,將每一個之前日 數...
指數平均數也叫EXPMA指標,它是一種趨向類指標,指數平均數指標是以指數式遞減加權的移動平均。其構造原理是對股票收盤價進行算術平均,並根據計算結果來進行分析,用於...
(Exponentially Weighted Moving-Average)指數加權移動平均值的控制圖。每個 EWMA 點都結合了來自之前所有子組或觀測值的信息。可以定製 EWMA 控制圖以檢測過程中任意...
