簡介
sigmoid函式也叫Logistic函式,用於隱層神經元輸出,取值範圍為(0,1),它可以將一個實數映射到(0,1)的區間,可以用來做二分類。在特徵相差比較複雜或是相差不是特別大時效果比較好。Sigmoid作為激活函式有以下優缺點:
優點:平滑、易於求導。
缺點:激活函式計算量大,反向傳播求誤差梯度時,求導涉及除法;反向傳播時,很容易就會出現梯度消失的情況,從而無法完成深層網路的訓練。
Sigmoid函式由下列公式定義
其對x的導數可以用自身表示:
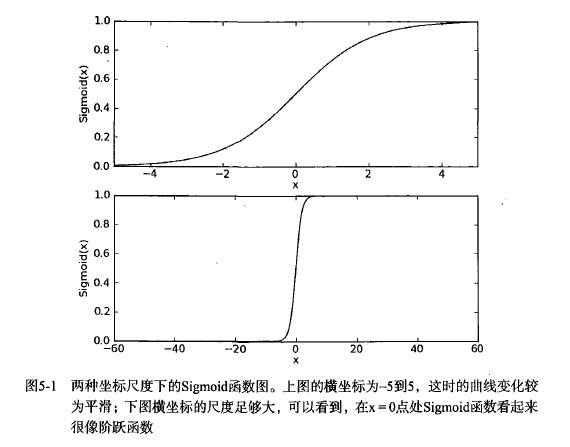
Sigmoid函式的圖形如S曲線
 Sigmoid 曲線
Sigmoid 曲線Sigmoid函式的級數表示:
激活函式
在計算機網路中,一個節點的激活函式定義了該節點在給定的輸入或輸入的集合下的輸出。標準的計算機晶片電路可以看作是根據輸入得到開(1)或關(0)輸出的數字電路激活函式。這與神經網路中的線性感知機的行為類似。然而,只有非線性激活函式才允許這種網路僅使用少量節點來計算非平凡問題。 在人工神經網路中,這個功能也被稱為傳遞函式。
sigmoid函式和tanh函式是研究早期被廣泛使用的2種
激活函式。兩者都為S 型飽和函式。 當sigmoid 函式輸入的值趨於正無窮或負無窮時,梯度會趨近零,從而發生梯度彌散現象。sigmoid函式的輸出恆為正值,不是以零為中心的,這會導致權值更新時只能朝一個方向更新,從而影響收斂速度。tanh 激活函式是sigmoid 函式的改進版,是以零為中心的對稱函式,收斂速度快,不容易出現 loss 值晃動,但是無法解決梯度彌散的問題。2個函式的計算量都是指數級的,計算相對複雜。softsign 函式是 tanh 函式的改進版,為 S 型飽和函式,以零為中心,值域為(−1,1)。
邏輯回歸
logistic回歸是一種廣義線性回歸(generalized linear model),因此與多重線性回歸分析有很多相同之處。它們的模型形式基本上相同,都具有 w‘x+b,其中w和b是待求參數,其區別在於他們的因變數不同,多重線性回歸直接將w‘x+b作為因變數,即y =w‘x+b,而logistic回歸則通過函式L將w‘x+b對應一個隱狀態p,p =L(w‘x+b),然後根據p 與1-p的大小決定因變數的值。如果L是logistic函式,就是logistic回歸,如果L是多項式函式就是多項式回歸。 logistic回歸的因變數可以是二分類的,也可以是多分類的,但是二分類的更為常用,也更加容易解釋,多類可以使用softmax方法進行處理。實際中最為常用的就是二分類的logistic回歸。Logistic回歸模型的適用條件:
1 因變數為二分類的分類變數或某事件的發生率,並且是數值型變數。但是需要注意,重複計數現象指標不適用於Logistic回歸。
2 殘差和因變數都要服從二項分布。二項分布對應的是分類變數,所以不是常態分配,進而不是用最小二乘法,而是最大似然法來解決方程估計和檢驗問題。
3 自變數和Logistic機率是線性關係
4 各觀測對象間相互獨立。
原理:如果直接將線性回歸的模型扣到Logistic回歸中,會造成方程二邊取值區間不同和普遍的非直線關係。因為Logistic中因變數為二分類變數,某個機率作為方程的因變數估計值取值範圍為0-1,但是,方程右邊取值範圍是無窮大或者無窮小。所以,才引入Logistic回歸。
Logistic回歸實質:發生機率除以沒有發生機率再取對數。就是這個不太繁瑣的變換改變了取值區間的矛盾和因變數自變數間的曲線關係。究其原因,是發生和未發生的機率成為了比值 ,這個比值就是一個緩衝,將取值範圍擴大,再進行對數變換,整個因變數改變。不僅如此,這種變換往往使得因變數和自變數之間呈線性關係,這是根據大量實踐而總結。所以,Logistic回歸從根本上解決因變數要不是連續變數怎么辦的問題。還有,Logistic套用廣泛的原因是許多現實問題跟它的模型吻合。例如一件事情是否發生跟其他數值型自變數的關係。
注意:如果自變數為字元型,就需要進行重新編碼。一般如果自變數有三個水平就非常難對付,所以,如果自變數有更多水平就太複雜。這裡只討論自變數只有三個水平。非常麻煩,需要再設二個新變數。共有三個變數,第一個變數編碼1為高水平,其他水平為0。第二個變數編碼1為中間水平,0為其他水平。第三個變數,所有水平都為0。實在是麻煩,而且不容易理解。最好不要這樣做,也就是,最好自變數都為連續變數。
實現
import numpy as npimport matplotlib.pyplot as pltdef sigmoid(x): return 1.0/(1+np.exp(-x))sigmoid_inputs = np.arange(-10,10,0.1)sigmoid_outputs = sigmoid(sigmoid_inputs)print("Sigmoid Function Input :: {}".format(sigmoid_inputs))print("Sigmoid Function Output :: {}".format(sigmoid_outputs))plt.plot(sigmoid_inputs,sigmoid_outputs)plt.xlabel("Sigmoid Inputs")plt.ylabel("Sigmoid Outputs")plt.show()

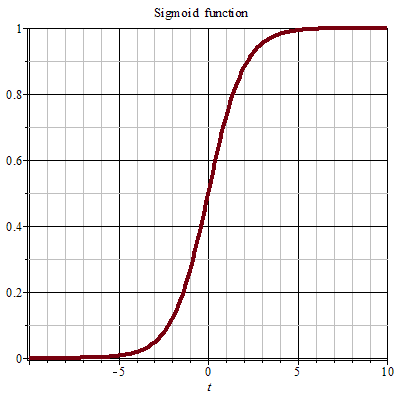
 Sigmoid 曲線
Sigmoid 曲線