基本介紹
- 中文名:L1範數正則化
- 外文名:L1 regularization
- 別名:稀疏規則運算元
定義


原理




























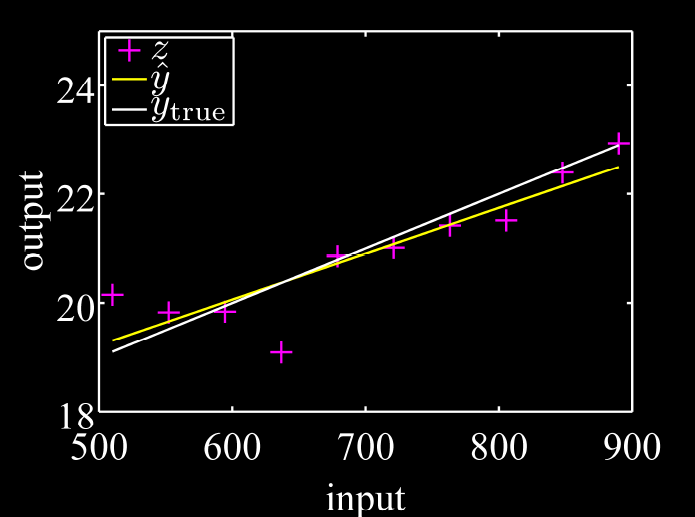






























L1範數正則化( L1 regularization 或 lasso )是機器學習(machine learning)中重要的手段,在支持向量機(support vector machine)學習過程中,實際是一種對於成...
L1正則化和L2正則化的區別 通過上面的分析,L1相對於L2能夠產生更加稀疏的模型,即當L1正則在參數w比較小的情況下,能夠直接縮減至0.因此可以起到特徵選擇的作用,該技術也稱之為 LASSO。如果從機率角度進行分析,很多範數約束相當於對...
L1範數罰具有產生稀疏模型的能力,使用L1範數罰作為正則化項的Lasso具有變數選擇功能和變數空間降維功能。實際上在Lasso之前已有能夠產生稀疏解的非負絞刑估計 (nonnegative garrote estimator)和橋回歸(bridge regression)模型被提出,但由於...
通過與合作醫院採集相關的心臟影像數據以及人體心電數據,採用高維有限元離散方法並進行多尺度數值求解,研究和分析了幾何模型離散對於結果精度的影響;通過分析心電逆問題的稀疏性質,提出基於有限元的L1範數正則化方法,克服不適定問題對結果...
項目的主要成果有:利用測度嵌套的思想建立了具有L1範數的可再生核巴拿赫空間理論,為發展機器學習中的L1稀疏逼近提供了理想的數學基礎;論證了基於此空間的L1係數正則化方法有稀疏誘導性,並能改進學習能力;建立了Lp(p>1)的可再生核...
克服節點型有限元方法中偶極子源奇異性等問題;(2)基於稀疏性分布特徵,提出了心臟向量模型和小波壓縮的心臟時空稀疏源模型;(3)提出了一個新型變分運算元用於有效獲取心臟等效雙層源的空間稀疏性特徵,並與L1範數正則化和疊代重加權範數...
這個方案的最佳化目標包括最小化分類誤差,表征誤差,權值的1範數(L1正則化)和分類器參數的2範數。 有監督的字典學習可以被視為一個三層神經網路(一層隱含層),第一層(輸入層)到第二層(隱含層)是表征學習,第二層到第三層(...
具體內容包括圖像的紋理和邊界同時恢復及算法,去除混合噪聲及模糊的模型和算法,受到乘性噪聲污染的快速兩步圖像恢複方法,圖像恢復模型中參數的選擇方法,圖像恢復的高斯平滑L1範數正則化方法,預處理方法在圖像恢復套用中的研究,圖像恢復...
8.1基於隱區域分割和權重L1範數正則化的圖像去霧(198)8.2基於吸收透射率補償及時空導向濾波的實時視頻去霧(208)參考文獻(219)第9章水下散射建模與處理(220)9.1基於光場成像的強散射水下圖像恢復(220)9.2基於雙透射率水...
考慮到生物發光光源相對於求解域的稀疏分布特性,我們將基於l2範數的正則化方法轉化為基於l1範數的稀疏正則化方法,提出了兩種基於稀疏正則化的光學三維重建方法:基於不完全變數的截斷共軛梯度法和初始對偶內點。同時,本項目也進行了一系列...
4.2正則化0 4.2.1L2範數正則化0 4.2.2L1範數正則化0 4.3Dropout0 4.4自適應學習率0 4.4.1AdaGrad0 4.4.2RMSProp0 4.4.3Adam0 4.5批標準化0 4.6用MindSpore 實現深度神經網路0 4.6.1各層參數說明0 4.6.2詳細...
4.4 基於L1範數的正則化軌跡擬合 4.5 空間mean-shift點追蹤 4.6 實驗結果分析 4.6.1 肺呼吸運動估計 4.6.2 肺滑動運動估計 4.6.3 運行時間 4.7 本章小結 第5章 基於L1範數與拓撲保持約束的點集匹配算法 5.1 ...
項目研究過程中,我們構造了具有L1範數的向量值再生核巴拿赫空間和具有group lasso 範數的向量值再生核巴拿赫空間,並套用於多目標機器學習問題;為深刻理解係數正則化所需要的再生核巴拿赫空間,我們提出了再生核巴拿赫空間一個統一的構造框架...
