基本介紹
- 中文名:K平均算法
- 外文名:k-means algorithm
- 處理:與最大期望算法很相似
- 發明於:1956年
簡介
算法描述
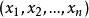
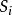
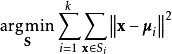
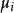
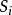
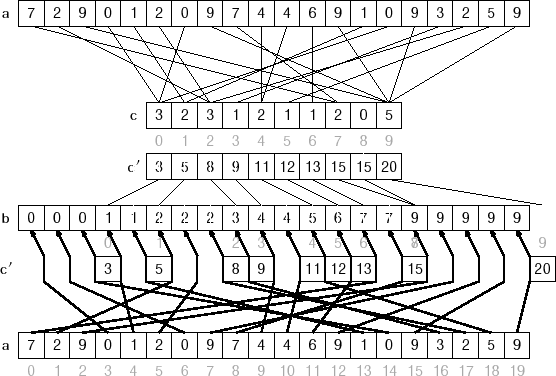
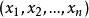
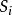
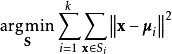
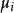
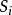
k平均聚類發明於1956年,是一個聚類算法,把n的對象根據他們的屬性分為k個分割,k < n。它與處理混合常態分配的最大期望算法很相似,因為他們都試圖找到數據中自然...
k均值聚類算法(k-means clustering algorithm)是一種疊代求解的聚類分析算法,其步驟是隨機選取K個對象作為初始的聚類中心,然後計算每個對象與各個種子聚類中心之間的...
K-MEANS算法是輸入聚類個數k,以及包含 n個數據對象的資料庫,輸出滿足方差最小標準k個聚類的一種算法。k-means 算法接受輸入量 k ;然後將n個數據對象劃分為 k...
K最近鄰(k-Nearest Neighbor,KNN)分類算法,是一個理論上比較成熟的方法,也是最簡單的機器學習算法之一。該方法的思路是:如果一個樣本在特徵空間中的k個最相似(...
k中心算法的基本過程是:首先為每個簇隨意選擇一個代表對象,剩餘的對象根據其與每個代表對象的距離(此處距離不一定是歐氏距離,也可能是曼哈頓距離)分配給最近的代表...
為了達到全局最優,基於劃分的聚類可能需要窮舉所有可能的劃分,計算量極大。實際上,大多數套用都採用了流行的啟發式方法,如k-均值和k-中心算法,漸近的提高聚類質量...
K-means算法是硬聚類算法,是典型的基於原型的目標函式聚類方法的代表,它是數據點到原型的某種距離作為最佳化的目標函式,利用函式求極值的方法得到疊代運算的調整規則。...
k-modes算法是在數據挖掘中對分類屬性型數據的採用的聚類算法。...... k-modes算法是對k-means算法的擴展。k-means算法是在數據挖掘領域中普遍套用的聚類算法,它...
K值是光散射式粉塵儀測定可吸入物的質量濃度時所用的質量濃度轉換係數。目錄1 質量濃度轉換係數K值 2 測定步驟 3 計算 4 確定K值的平均值 5 已知K值時可...
鄰近算法,或者說K最近鄰(kNN,k-NearestNeighbor)分類算法是數據挖掘分類技術中最簡單的方法之一。所謂K最近鄰,就是k個最近的鄰居的意思,說的是每個樣本都可以用...
時刻系統調度優先權最大的用戶,比例公平算法的數學表達式可以參考式(2),其中k是被調度用戶,Ri(t)為用戶i在t時刻請求的速率,Ti(t)為用戶i在t時刻的累積平均...
設原始數據為被分成K組,各組的組中的值為X1,X2,...,Xk,各組的頻數分別為f1,f2,...,fk,加權算術平均數的計算公式為:[2] 特殊說明 1. 加權算術平均...
1 K值計算方式: 2 影響K值的因素: K值K值計算方式: 編輯 時間t1測OCV1時間t2測OCV2K=(OCV1-OCV2)/(t2-t1)做的比較好的電池K值一般小於2mV/d或0....
隨機算法重要方法 Monte Carlo求定積分法隨機K-選擇法隨機快排序...時間複雜性,是對確定實例I的期望運行時間,即反覆地運行實例I,所取的平均運行...
派系過濾算法[2] (cliquepercolationmethod,CPM)認為社區是具有共享節點的全連通子圖集合,並通過一種團過濾算法來識別網路中的社區結構。算法首先搜尋所有具有k個節點...
移動平均值,就是指定時間段,對時間序列數據進行移動計算平均值。移動平均值常...(2)當序列包含周期性變動時,移動平均的項數k應與周期長度一致。這樣才能在消除...
在這個表格中,n是要被排序的紀錄數量以及k是不同鍵值的數量。排序算法穩定的 ...冒泡排序的平均時間複雜度與插入排序相同,也是平方級的,但冒泡排序是原地排序的,...
PageRank算法中對於向外連結的權值貢獻是平均的,也就是不考慮不同連結的重要性...假定主機A上有k個網頁指向主機B上的某個文檔d,則A上的k個文檔對B的...
所以要計算某個分子的平均相對分子質量,我們只要用周期表查出這個物質種每個原子的原子量相加就可以了,要計算相對分子質量,當題目沒有特別給出該分子種原子的原子量...
按外牆各部位(不包括門窗)的傳熱係數對其面積的加權平均計算求得,單位:W/(m2·K)。當外牆的主牆體與外牆中的構造柱、圈樑、樓板端頭等周邊熱橋採用不同材料時,...
由於其易於計算和其他期望的特徵,樣本平均數廣泛用於統計和套用中,以表示分布的位置。 [1] 樣本平均數計算方法 編輯 設xij是第j個隨機變數(j = 1,...,K)的...
點的一個真實的數據對象來代表該簇的,而K-Medoids算法是用計算出來的簇中對象的平均值來代表該簇的,這個平均值是虛擬的,並沒有一個真實的數據對象具有這些平均...
假設我們已經通過一定算法,將待分類數據進行了聚類。常用的比如使用K-means ,將...將所有點的輪廓係數求平均,就是該聚類結果總的輪廓係數。a(i) :i向量到同一...
(1) 從 n個數據對象任意選擇 k 個對象作為初始聚類中心; (2) 循環(3)到(4)直到每個聚類不再發生變化為止 (3) 根據每個聚類對象的均值(中心對象),計算每個...
