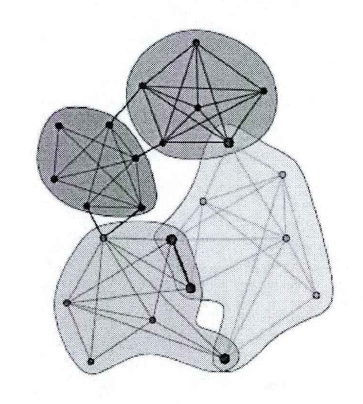
CPM算法是最早的重疊社區發現算法,它的思想是基於團滲透理論的。算法在二分圖、有向圖及加權圖中均已有所套用。CFinder是G.Palla等基於CPM算法開發的一個自由軟體,它不僅能非常有效地定位和可視化處理大規模稀疏網路社群,而且還可用於定量描述社會網路的演變。
基本介紹
- 中文名:派系過濾算法
- 外文名:CPM
- 時間:2005
算法原理:
派系過濾算法(cliquepercolationmethod,CPM)認為社區是具有共享節點的全連通子圖集合,並通過一種團過濾算法來識別網路中的社區結構。算法首先搜尋所有具有k個節點的完全子圖,而後建立以k-clique為節點的新圖,在該圖中如果兩個k-clique有(k-1)個公共節點則在新圖中為代表他們的節點間建立一條邊。最終在新圖中,每個連通子圖即為一個社團。
算法主要步驟:
1)找到網路中的所有團,構造一個團團重疊矩陣,矩陣是對稱的,矩陣的第i行第j列即ccom[i][j]表示第i個團和第j個團的公共節點數。
2)給定參數k,將團團矩陣中非對角線上元素小於k-1,且對角線上元素小於k的所有項置0,其他的元素為1;這樣,所有對角線為1的團為k團,而非對角線為1的團i、團j是相鄰的。通過這個矩陣可以得到相應的社區。
注意:
由於k是個輸入參數值,從而k的取值將會影響CPM算法的最終社區發現結果,當k取值越小社區將會越大,且社區結構為稀疏。但是實驗證明k的取值影響不是很大,一般值為4到6。然而,由於該算法是基於完全子圖,因此比較適用於完全子圖比較多的網路,即邊密集的網路,對於稀疏網路效率將會很低,且該算法還無法分配完全子圖外的頂點。