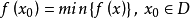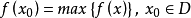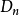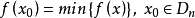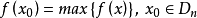基本概念
最最佳化問題
最最佳化(Optimization),就是在複雜環境中遇到的許多可能的決策中,挑選“最好”的決策的科學。
例如,工程設計中,怎樣選擇設計參數,使得設計方案能以儘量低的成本預算滿足設計要求;資源分配中,怎樣分配有限資源,使得在滿足各方面需求的情況下最大化經濟效益;生產安排中,怎樣選擇生產方案能在產量、質量和利潤中找到符合要求的平衡點;還有在城市規劃、軍事指揮、生活安排等方方面面都存在著最最佳化問題。
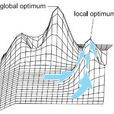
全局最優
針對一定條件/環境下的一個問題/目標,若一項決策和所有解決該問題的決策相比是最優的,就可以被稱為全局最優。
將上述定義用數學公式表示為:在無限制環境集合R內,假設限制條件/環境為集合D(D包含於R),問題代價或目標函式為f(x),其中x指決策,那么全局最優就是指決策滿足
或
其中對目標函式去最大值還是最小值根據具體問題和要求而確定。
局部最優
和全局最優不同,局部最優不要求在所有決策中是最好的。
針對一定條件/環境下的一個問題/目標,若一項決策和部分解決該問題的決策相比是最優的,就可以被稱為局部最優。
將上述定義用數學公式表示為:按照上一節的定義,對於D內的一個子集
,局部最優就是指決策滿足
或
可以看到,局部最優不一定是全局最優,全局最優一定是局部最優。
最最佳化問題
最最佳化問題類型
根據不同的劃分角度,最最佳化問題可以劃分為不同的類型,對幾個常用的類別舉例如下。
針對是否有約束條件D,可以劃分為無約束最最佳化問題和有約束最最佳化問題;
針對目標數,可以劃分為單目標最佳化問題和多目標最佳化問題;
最最佳化問題解法
對不同的最最佳化問題,有不同的決策方法和算法。
對於有約束條件的最最佳化問題,由於一般的問題可以用線性方程表示(或者說約束條件是線性的),所以最常見的解決算法是線性規劃;對於一些複雜的問題,可能會用到非線性方程,此時就需要使用非線性規劃。線性規劃有
單純形法、對偶解法、修正的單純形法等具體算法;非線性規劃對於只含等式、含不等式、凸最佳化、多目標最佳化等不同情況也有不同的解法。
局部最優
局部最優的產生
一般的啟發式算法、貪婪算法或局部算法都很容易產生局部最優,或者說根本無法查證產生的最優解是否是全局的,或者只是局部的。這是因為對於大型系統或複雜的問題,一般的算法都著眼於從局部展開求解,以減少計算量和算法複雜度。
局部最優的意義
對於最佳化問題,尤其是最最佳化問題,總是希望找到全局最優的解或策略,但是當問題的複雜度過於高,要考慮的因素和處理的信息量過多的時候,我們往往會傾向於接受局部最優解,因為局部最優解的質量不一定都是差的。尤其是當我們有確定的評判標準標明得出的解是可以接受的話,通常會接收局部最優的結果。這樣,從成本、效率等多方面考慮,才是實際工程中會採取的策略。
局部最優的避免
在部分工程領域,受限於時間和成本,對局部最優和全局最優可能不會進行嚴格的檢查,但是有的情況下式要求得到全局最優的,這是就需要避免產生僅僅是局部最優的結果。
對局部最優的避免有兩個根本方法:
深入研究問題的機理,對問題的機理研究的越透徹,就能更準確的找到全局最優,或劃定全局最優可能的區域;
隨機搜尋,對機理不明的問題,解的搜尋越隨機陷入局部最優的可能性就越小。
對於已經陷入局部最優,或懷疑陷入局部最優的情況,一般是採取“跳出”或“重啟”兩種手段,也就是在當前解的基礎上向其他方向搜尋,或者無視當前解並在新的區域重新搜尋。