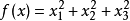粒子群算法

粒子群算法，也稱粒子群最佳化算法或鳥群覓食算法（Particle Swarm Optimization），縮寫為 PSO， 是由J. Kennedy和R. C. Eberhart等開發的一種新的進化算法(Evolutionary Algorithm - EA)。PSO 算法屬於進化算法的一種，和模擬退火算法相似，它也是從隨機解出發，通過疊代尋找最優解，它也是通過適應度來評價解的品質，但它比遺傳算法規則更為簡單，它沒有遺傳算法的“交叉”(Crossover) 和“變異”(Mutation) 操作，它通過追隨當前搜尋到的最優值來尋找全局最優。這種算法以其實現容易、精度高、收斂快等優點引起了學術界的重視，並且在解決實際問題中展示了其優越性。粒子群算法是一種並行算法。

基本介紹

• 中文名：粒子群算法
• 外文名：Particle Swarm Optimization
• 別名：鳥群覓食算法
• 縮寫：PSO
• 提出時間：1995年
• 提出者：J. Kennedy和R. C. Eberhart等
• 套用：神經網路、遺傳算法等

簡介

粒子群最佳化算法(PSO)是一種進化計算技術(evolutionary computation)，1995 年由Eberhart 博士和kennedy 博士提出，源於對鳥群捕食的行為研究 。該算法最初是受到飛鳥集群活動的規律性啟發，進而利用群體智慧型建立的一個簡化模型。粒子群算法在對動物集群活動行為觀察基礎上，利用群體中的個體對信息的共享使整個群體的運動在問題求解空間中產生從無序到有序的演化過程，從而獲得最優解。

起源

如前所述，PSO模擬鳥群的捕食行為。構想這樣一個場景：一群鳥在隨機搜尋食物。在這個區域裡只有一塊食物。所有的鳥都不知道食物在那裡。但是他們知道當前的位置離食物還有多遠。那么找到食物的最優策略是什麼呢。最簡單有效的就是搜尋目前離食物最近的鳥的周圍區域。

PSO從這種模型中得到啟示並用於解決最佳化問題。PSO中，每個最佳化問題的解都是搜尋空間中的一隻鳥。我們稱之為“粒子”。所有的粒子都有一個由被最佳化的函式決定的適應值(fitness value)，每個粒子還有一個速度決定他們飛翔的方向和距離。然後粒子們就追隨當前的最優粒子在解空間中搜尋。

PSO 初始化為一群隨機粒子(隨機解)。然後通過疊代找到最優解。在每一次疊代中，粒子通過跟蹤兩個"極值"來更新自己。第一個就是粒子本身所找到的最優解，這個解叫做個體極值pBest。另一個極值是整個種群目前找到的最優解，這個極值是全局極值gBest。另外也可以不用整個種群而只是用其中一部分作為粒子的鄰居，那么在所有鄰居中的極值就是局部極值。

粒子公式：

在找到這兩個最優值時，粒子根據如下的公式來更新自己的速度和新的位置：

v[] = w * v[] + c1 * rand() * (pbest[] - present[]) + c2 * rand() * (gbest[] - present[]) (a)

present[] = present[] + v[] (b)

v[] 是粒子的速度, w是慣性權重,present[] 是當前粒子的位置. pbest[] and gbest[] 如前定義. rand () 是介於（0， 1）之間的隨機數. c1, c2 是學習因子. 通常 c1 = c2 = 2.

程式的偽代碼如下

For each particle

____Initialize particle

END

Do

____For each particle

________Calculate fitness value

________If the fitness value is better than the best fitness value (pBest) in history

____________set current value as the new pBest

____End

____Choose the particle with the best fitness value of all the particles as the gBest

____For each particle

________Calculate particle velocity according equation (a)

________Update particle position according equation (b)

____End

While maximum iterations or minimum error criteria is not attained

在每一維粒子的速度都會被限制在一個最大速度Vmax，如果某一維更新後的速度超過用戶設定的Vmax，那么這一維的速度就被限定為Vmax

套用

PSO同遺傳算法類似，是一種基於疊代的最佳化算法。系統初始化為一組隨機解，通過疊代搜尋最優值。但是它沒有遺傳算法用的交叉(crossover)以及變異(mutation)，而是粒子在解空間追隨最優的粒子進行搜尋。同遺傳算法比較，PSO的優勢在於簡單容易實現並且沒有許多參數需要調整。目前已廣泛套用於函式最佳化，神經網路訓練，模糊系統控制以及其他遺傳算法的套用領域。

近年來，一些學者將PSO算法推廣到約束最佳化問題，其關鍵在於如何處理好約束，即解的可行性。如果約束處理的不好，其最佳化的結果往往會出現不能夠收斂和結果是空集的狀況。基於PSO算法的約束最佳化工作主要分為兩類：

（1）罰函式法。罰函式的目的是將約束最佳化問題轉化成無約束最佳化問題。

（2）將粒子群的搜尋範圍都限制在條件約束簇內，即在可行解範圍內尋優。

根據文獻介紹，Parsopoulos等採用罰函式法，利用非固定多段映射函式對約束最佳化問題進行轉化，再利用PSO算法求解轉化後問題，仿真結果顯示PSO算法相對遺傳算法更具有優越性，但其罰函式的設計過於複雜，不利於求解；Hu等採用可行解保留政策處理約束，即一方面更新存儲中所有粒子時僅保留可行解，另一方面在初始化階段所有粒子均從可行解空間取值，然而初始可行解空間對於許多問題是很難確定的；Ray等提出了具有多層信息共享策略的粒子群原理來處理約束，根據約束矩陣採用多層Pareto排序機制來產生優良粒子，進而用一些優良的粒子來決定其餘個體的搜尋方向。

但是，目前有關運用PSO算法方便實用地處理多約束目標最佳化問題的理論成果還不多。處理多約束最佳化問題的方法有很多，但用PSO算法處理此類問題目前技術並不成熟，這裡就不介紹了。

比較

演化計算技術

大多數演化計算技術都是用同樣的過程：

1.種群隨機初始化；

2.對種群內的每一個個體計算適應值(fitness value)，適應值與最優解的距離直接有關；

3.種群根據適應值進行複製；

4.如果終止條件滿足的話，就停止，否則轉步驟2。

從以上步驟，我們可以看到PSO和GA有很多共同之處。兩者都隨機初始化種群，而且都使用適應值來評價系統，而且都根據適應值來進行一定的隨機搜尋。兩個系統都不是保證一定找到最優解 。

記憶

PSO沒有遺傳操作如交叉(crossover)和變異(mutation)，而是根據自己的速度來決定搜尋。粒子還有一個重要的特點，就是有記憶。

與遺傳算法比較, PSO 的信息共享機制是很不同的。在遺傳算法中，染色體(chromosomes) 互相共享信息，所以整個種群的移動是比較均勻的向最優區域移動。在PSO中, 只有gBest (or pBest) 給出信息給其他的粒子，這是單向的信息流動。整個搜尋更新過程是跟隨當前最優解的過程。

與遺傳算法比較，在大多數的情況下，所有的粒子可能更快的收斂於最優解。

訓練過程

這裡用一個簡單的例子說明PSO訓練神經網路的過程。這個例子使用分類問題的基準函式(Benchmark function)IRIS數據集。(Iris 是一種鳶尾屬植物) 在數據記錄中，每組數據包含Iris花的四種屬性：萼片長度，萼片寬度，花瓣長度，和花瓣寬度，三種不同的花各有50組數據。這樣總共有150組數據或模式。

我們用3層的神經網路來做分類。現在有四個輸入和三個輸出。所以神經網路的輸入層有4個節點，輸出層有3個節點我們也可以動態調節隱含層節點的數目，不過這裡我們假定隱含層有6個節點。我們也可以訓練神經網路中其他的參數。不過這裡我們只是來確定網路權重。粒子就表示神經網路的一組權重，應該是4*6+6*3=42個參數。權重的範圍設定為[-100，100] (這只是一個例子，在實際情況中可能需要試驗調整)。在完成編碼以後，我們需要確定適應函式。對於分類問題，我們把所有的數據送入神經網路，網路的權重由粒子的參數決定。然後記錄所有的錯誤分類的數目作為那個粒子的適應值。現在我們就利用PSO來訓練神經網路來獲得儘可能低的錯誤分類數目。PSO本身並沒有很多的參數需要調整。所以在實驗中只需要調整隱含層的節點數目和權重的範圍以取得較好的分類效果。

從上面的例子我們可以看到套用PSO解決最佳化問題的過程中有兩個重要的步驟：問題解的編碼和適應度函式。

不需要像遺傳算法一樣是二進制編碼(或者採用針對實數的遺傳操作）。例如對於問題求解，粒子可以直接編碼為, 而適應度函式就是f(x)。接著我們就可以利用前面的過程去尋優。這個尋優過程是一個疊代過程，中止條件一般為設定為達到最大循環數或者最小錯誤。

PSO中並沒有許多需要調節的參數，下面列出了這些參數以及經驗設定：

粒子數：一般取 20–40，其實對於大部分的問題10個粒子已經足夠可以取得好的結果，不過對於比較難的問題或者特定類別的問題，粒子數可以取到100 或 200。

粒子的長度：這是由最佳化問題決定，就是問題解的長度。

粒子的範圍：由最佳化問題決定，每一維可以設定不同的範圍。

V_max：最大速度決定粒子在一個循環中最大的移動距離，通常設定為粒子的範圍寬度。例如上面的例子裡，粒子，x₁屬於[-10,10]，那么V_max的大小就是20。

學習因子：c₁和c₂通常等於2，不過在文獻中也有其他的取值。但是一般c₁等於c₂並且範圍在0和4之間。

中止條件：最大循環數以及最小錯誤要求。例如，在神經網路訓練例子中，最小錯誤可以設定為1個錯誤分類，最大循環設定為2000，這箇中止條件由具體的問題確定。

全局PSO和局部PSO：前者速度快不過有時會陷入局部最優，後者收斂速度慢一點不過很難陷入局部最優。在實際套用中，可以先用全局PSO找到大致的結果，再用局部PSO進行搜尋。

另外的一個參數是慣性權重，Shi 和Eberhart指出(A modified particle swarm optimizer,1998)：當V_max很小時（對schaffer的f6函式，Vmax<=2），使用接近於1的慣性權重；當V_max不是很小時（對schaffer的f6函式，Vmax>=3），使用權重w=0.8較好。如果沒有V_max的信息，使用0.8作為權重也是一種很好的選擇。慣性權重w很小時偏重於發揮粒子群算法的局部搜尋能力；慣性權重很大時將會偏重於發揮粒子群算法的全局搜尋能力。

實現C++代碼

代碼來自2008年數學建模東北賽區B題，

#include"stdafx.h"#include<math.h>#include<time.h>#include<iostream>#include<fstream>usingnamespacestd;intc1=2;//加速因子intc2=2;//加速因子doublew=1;//慣性權重doubleWmax=1;//最大慣性權重doubleWmin=0.6;//最小慣性權重intKmax=110;//疊代次數intGdsCnt;//物資總數intconstDim=10;//粒子維數intconstPNum=50;//粒子個數intGBIndex=0;//最優粒子索引doublea=0.6;//適應度調整因子doubleb=0.5;//適應度調整因子intXup[Dim];//粒子位置上界數組intXdown[Dim]=;//粒子位置下界數組intValue[Dim];//初始急需度數組intVmax[Dim];//最大速度數組classPARTICLE;//申明粒子節點voidCheck(PARTICLE&,int);//約束函式voidInput(ifstream&);//輸入變數voidInitial();//初始化相關變數doubleGetFit(PARTICLE&);//計算適應度voidCalculateFit();//計算適應度voidBirdsFly();//粒子飛翔voidRun(ofstream&,int=2000);//運行函式classPARTICLE//微粒類{public:intX[Dim];//微粒的坐標數組intXBest[Dim];//微粒的最好位置數組intV[Dim];//粒子速度數組doubleFit;//微粒適合度doubleFitBest;//微粒最好位置適合度};PARTICLEParr[PNum];//粒子數組intmain()//主函式{ofstreamoutf("out.txt");ifstreaminf("data.txt");//關聯輸入檔案inf>>GdsCnt;//輸入物資總數Input(inf);Initial();Run(outf,100);system("pause");return0;}voidCheck(PARTICLE&p,intcount)//參數:p粒子對象,count物資數量{srand((unsigned)time(NULL));intsum=0;for(inti=0;i<Dim;i++){if(p.X>Xup)p.X=Xup;elseif(p.X<Xdown)p.X=Xdown;if(p.V>Vmax)p.V=Vmax;elseif(p.V<0)p.V=0;sum+=p.X;}while(sum>count){p.X[rand()%Dim]--;sum=0;for(inti=0;i<Dim;i++){if(p.X>Xup)p.X=Xup;elseif(p.X<Xdown)p.X=Xdown;if(p.V>Vmax)p.V=Vmax;elseif(p.V<0)p.V=0;sum+=p.X;}}voidInput(ifstream&inf)//以inf為對象輸入數據{for(inti=0;i<Dim;i++)inf>>Xup;for(inti=0;i<Dim;i++)inf>>Value;}voidInitial()//初始化數據{GBIndex=0;srand((unsigned)time(NULL));//初始化隨機函式發生器for(inti=0;i<Dim;i++)Vmax=(int)((Xup-Xdown)*0.035);for(inti=0;i{for(intj=0;j<Dim;j++){Parr.X[j]=(int)(rand()/(double)RAND_MAX*(Xup[j]-Xdown[j])-Xdown[j]+0.5);Parr.XBest[j]=Parr.X[j];Parr.V[j]=(int)(rand()/(double)RAND_MAX*(Vmax[j]-Vmax[j]/2));}Parr.Fit=GetFit(Parr);Parr.FitBest=Parr.Fit;if(Parr.Fit>Parr[GBIndex].Fit)GBIndex=i;}}doubleGetFit(PARTICLE&p)//計算對象適應度{doublesum=0;for(inti=0;i<Dim;i++)for(intj=1;j<=p.X;j++)sum+=(1-(j-1)*a/(Xup-b))*Value;returnsum;}voidCalculateFit()//計算數組內各粒子的適應度{for(inti=0;i{Parr.Fit=GetFit(Parr);}}voidBirdsFly()//粒子飛行尋找最優解{srand((unsigned)time(NULL));staticintk=10;w=Wmax-k*(Wmax-Wmin)/Kmax;k++;for(inti=0;i{for(intj=0;j<Dim;j++){Parr.V[j]=(int)(w*Parr.V[j]);Parr.V[j]+=(int)(c1*rand()/(double)RAND_MAX*(Parr.XBest[j]-Parr.X[j]);Parr.V[j]+=c2*rand()/(double)RAND_MAX*(Parr[GBIndex].XBest[j]-Parr.X[j]));}}Check(Parr,GdsCnt);for(intj=0;j<Dim;j++){Parr.X[j]+=Parr.V[j];Check(Parr,GdsCnt);}CalculateFit();for(inti=0;i{if(Parr.Fit>=Parr.FitBest){Parr.FitBest=Parr.Fit;for(intj=0;j<Dim;j++)Parr.XBest[j]=Parr.X[j];}}GBIndex=0;for(inti=0;i{if(Parr.FitBest>Parr[GBIndex].FitBest&&i!=GBIndex)GBIndex=i;}}voidRun(ofstream&outf,intnum)//令粒子以規定次數num飛行{for(inti=0;i<num;i++){BirdsFly();outf<<(i+1)<<ends<for(intj=0;j<Dim;j++)outf<outf<<endl;}cout<<"Done!"<<endl;}