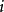黎曼不變數

黎曼不變數是在守恆方程系統上進行的數學變換，使它們更容易得解。一般外流求解的遠場邊界條件的確定用的是黎曼不變數，黎曼不變數是把歐拉方程解耦得到的變數，解耦的一般方法就是把歐拉方程源變數前的矩陣對角化。

基本介紹

• 中文名：黎曼不變數
• 外文名：Riemann invariants
• 分類：計算機 自動化
• 提出：伯恩哈德·黎曼
• 系統：守恆方程系統
• 實質：特徵變數
• 推導：歐拉方程

定義

黎曼不變數是在守恆方程系統上進行的數學變換，使它們更容易得解。在得偏微分方程特徵曲線上，黎曼不變數是常數。最初是由伯恩哈德黎曼在研究氣體動力學中的平面波工作中提出的。

先寫一組一維歐拉方程：

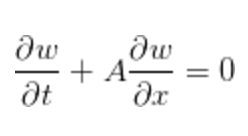
其中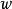，可以是守恆變數也可以是原始變數，特徵值是一樣的。

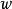
相似變換：

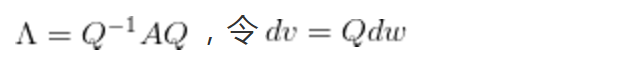
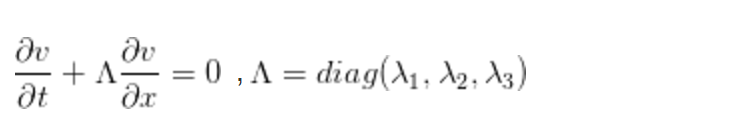
把上式寫成單方程形式：

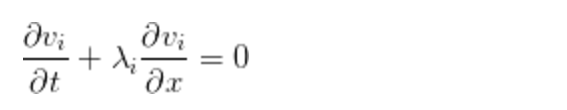
這是相容關係。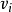就是所謂的特徵變數。歐拉方程有3個特徵變數，只有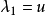對應的相容關係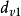有解析解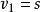，（熵）。注意，另外兩個相容關係沒有解析解，因為三個特徵值是耦合的。不過如果假設 整個流場都是等熵的，。

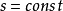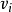
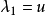
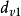
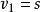
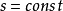
那么可以另外兩個相容關係也可以得到解析解：

這兩個就是所謂的黎曼不變數，在套用中有時這三個都可以叫做Riemann不變數。

套用

二維和三維情況下黎曼不變數

上面是基於一維歐拉方程推的，二維情況下比一維多一個方程，也多一個特徵值，有4個。現在必須把這第四個黎曼不變數找出來。

第一種方法：用到一個概念，被動標量。

取遠場邊界局部坐標系：令法向速度為u，切向速度為v。把v當做是一個類似於溫度T的標量。因此可以直接寫出第四個方程：

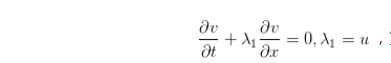
第四個特徵變數為切向速度 v。

第二種方法：

類似於前面推導黎曼不變數的方法，直接將二維歐拉方程進行相似變換（對角化），也得到相似的結論。

所以二維情況下，有4個特徵值，對應四個特徵變數（黎曼不變數）：

三維也可以類比出來，只是有兩個切向分速度而已，都可以作為被動標量，特徵值也是u。

遠場邊界條件

上面推倒的是類比一維情況的，特徵變數在遠場邊界的法向傳播，特徵值表征傳播方向和速度。以二維為例，假設法向速度u，切向速度v，此時根據具體流體情況可以分為以下四類：

亞聲速入流 0<u<c（規定速度往內流為正，隨便規定）

如果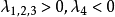，這說明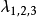對應的特徵變數由外界通過遠場邊界往內傳播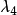，對應的特徵變數由流場內通過遠場邊界往外傳播。所以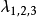，對應的遠場邊界上特徵變數和流場外的相同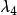，對應的遠場邊界上特徵變數和流場內的相同。

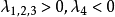
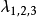
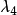
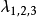
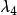
記流場外物理量(已知)下標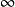，流場內物理量(已知)下標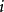，遠場邊界物理量(待求)下標。

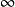
則有：

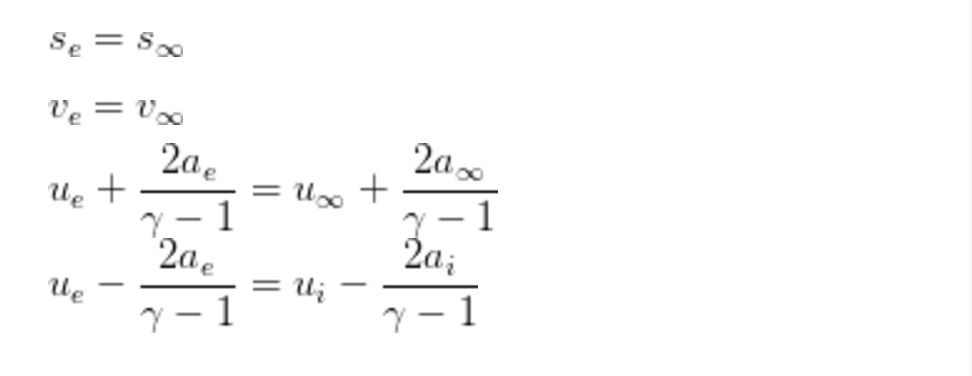
遠場邊界需要得到什麼？速度，兩個熱力學量（就可以得到其他所有熱力學量）。

通過上面4個式子，確實可以得到速度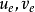： ；也確實可以得到兩個熱力學量：。

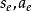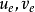
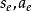
亞聲速出流，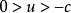

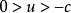
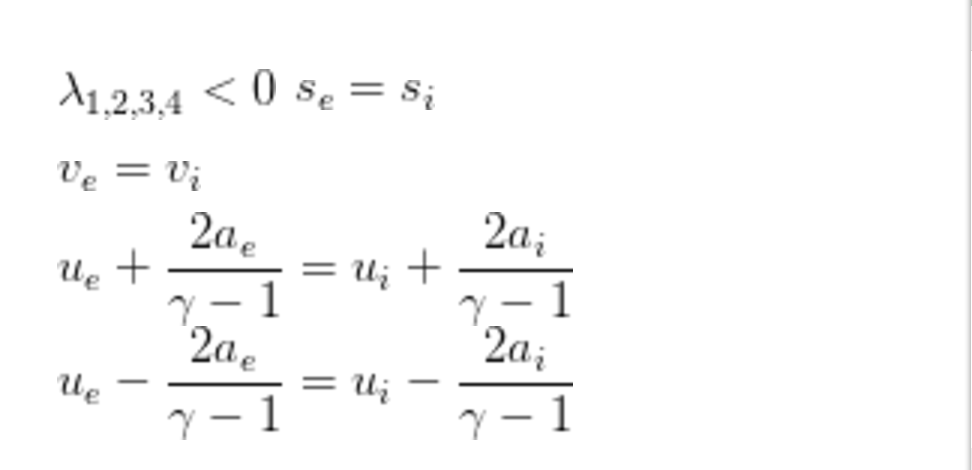
超聲速入流，

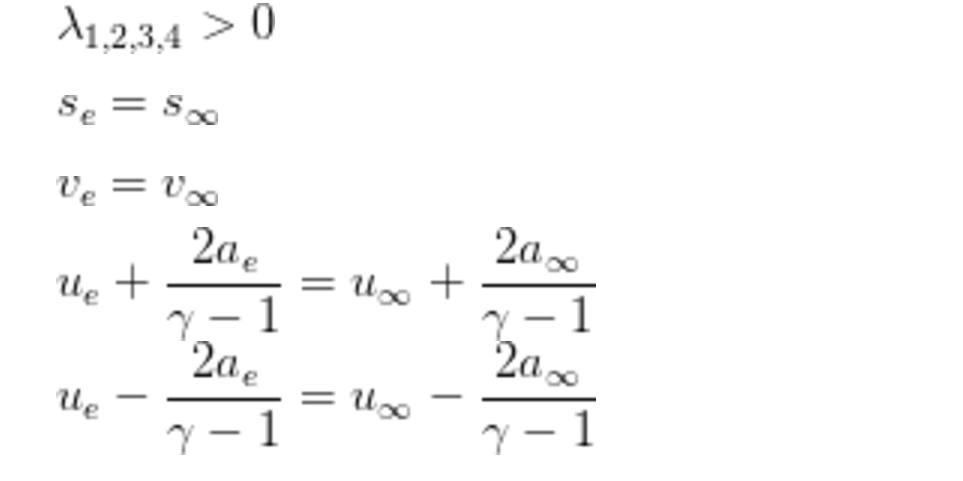
超聲速出流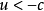

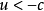
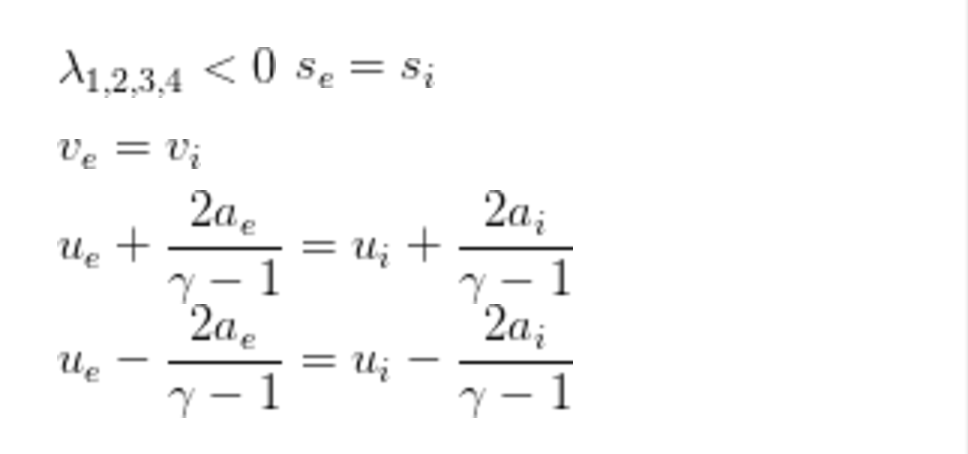
這就是遠場邊界條件，凡是下標為的量都是必須提前給定的，下標為的都是不需要給定的。

一些商業軟體提供的遠場邊界條件不一樣，但是一定可以通過計算轉換歸結到這上來，可以算一下不同情況下需要給定的遠場邊界條件個數（一個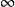 算一個）。有時候可能還會看到某些遠場邊界條件，比如超聲速出口的零法向梯度條件。嚴格來說，這不算邊界條件，這只是計算下標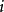對應物理量的一種指定，可以完全不提供這個選擇。