黃金比例分割

黃金比例分割是指把一條線段分割為兩部分，使其中一部分與全長之比等於另一部分與這部分之比。其比值是一個無理數，取其前三位數字的近似值是0.618。

基本介紹

• 中文名：黃金比例分割、黃金分割比例
• 外文名：Golden Ratio
• 精確值：2分之（（根號5）-1）
• 特點：黃金分割數是無理數

簡介

由於按此比例設計的造型十分美麗，因此稱為黃金分割，也稱為中外比。這是一個十分有趣的數字，以0.618來近似，通過簡單的計算就可以發現：黃金分割奇妙之處，在於其與1的和與其倒數是相等的。例如：1.618的倒數是0.618，而1.618:1與1:0.618是一樣的。其實這說明黃金比是方程x的平方+x-1=0的正數解。

方程式

確切值為(√5-1)/2，黃金分割數是無理數。

這個數值的作用不僅僅體現在諸如繪畫、雕塑、音樂、建築等藝術領域，而且在管理、工程設計等方面也有著不可忽視作用。

來歷

2000多年前,古希臘雅典學派的第三大算學家歐道克薩斯首先提出黃金分割。所謂黃金分割，指的是把長為L的線段分為兩部分，使其中一部分對於全部之比，等於另一部分對於該部分之比。而計算黃金分割最簡單的方法，是計算斐波那契數列1，1，2，3，5，8，13，21，...後二數之比2/3,3/5,5/8,8/13,13/21,...近似值的。

發現歷史

由於公元前6世紀古希臘的畢達哥拉斯學派研究過正五邊形和正十邊形的作圖，因此現代數學家們推斷當時畢達哥拉斯學派已經觸及甚至掌握了黃金分割。

公元前4世紀，古希臘數學家歐多克索斯第一個系統研究了這一問題，並建立起比例理論。

公元前300年前後歐幾里得撰寫《幾何原本》時吸收了歐多克索斯的研究成果，進一步系統論述了黃金分割，成為最早的有關黃金分割的論著。

中世紀後，黃金分割被披上神秘的外衣，義大利數家帕喬利稱中末比為神聖比例，並專門為此著書立說。德國天文學家克卜勒稱黃金分割為神聖分割。

到19世紀黃金分割這一名稱才逐漸通行。黃金分割數有許多有趣的性質，人類對它的實際套用也很廣泛。最著名的例子是優選學中的黃金分割法或0.618法，是由美國數學家基弗於1953年首先提出的，70年代在中國推廣，當時套用於科學實驗，成為“優選法”。

文藝復興

黃金分割在文藝復興前後，經過阿拉伯人傳入歐洲，受到了歐洲人的歡迎，他們稱之為"金法"，17世紀歐洲的一位數學家，甚至稱它為"各種算法中最可寶貴的算法"。這種算法在印度稱之為"三率法"或"三數法則"，也就是我們常說的比例方法。

其實有關"黃金分割"，我國也有記載。雖然沒有古希臘的早，但它是我國古代數學家獨立創造的，後來傳入了印度。經考證。歐洲的比例算法是源於我國而經過印度由阿拉伯傳入歐洲的，而不是直接從古希臘傳入的。

因為它在造型藝術中具有美學價值，在工藝美術和日用品的長寬設計中，採用這一比值能夠引起人們的美感，在實際生活中的套用也非常廣泛，建築物中某些線段的比就科學採用了黃金分割，舞台上的報幕員並不是站在舞台的正中央，而是偏在台上一側，以站在舞台長度的黃金分割點的位置最美觀，聲音傳播的最好。就連植物界也有採用黃金分割的地方，如果從一棵嫩枝的頂端向下看，就會看到葉子是按照黃金分割的規律排列著的。在很多科學實驗中，選取方案常用一種0.618法，即優選法，它可以使我們合理地安排較少的試驗次數找到合理的西方和合適的工藝條件。正因為它在建築、文藝、工農業生產和科學實驗中有著廣泛而重要的套用，所以人們才珍貴地稱它為"黃金分割"。

黃金分割〔Golden Section〕是一種數學上的比例關係。黃金分割具有嚴格的比例性、藝術性、和諧性，蘊藏著豐富的美學價值。套用時一般取0.618 ，就像圓周率在套用時取3.14一樣。

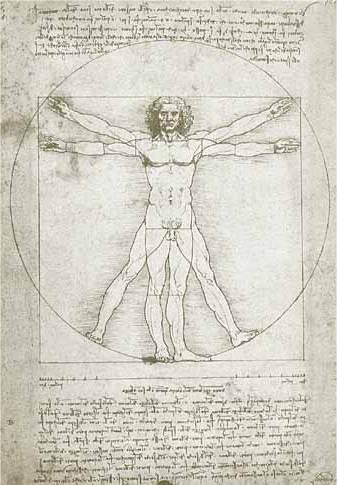
黃金矩形(Golden Rectangle)的長寬之比為黃金分割率,換言之,矩形的長邊為短邊 1.618倍.黃金分割率和黃金矩形能夠給畫面帶來美感,令人愉悅.在很多藝術品以及大自然中都能找到它.希臘雅典的帕撒神農廟就是一個很好的例子,他的《維特魯威人》符合黃金矩形.《蒙娜麗莎》的臉也符合黃金矩形,《最後的晚餐》同樣也套用了該比例布局.

證明方法

設一條線段AB的長度為a，C點在靠近B點的黃金分割點上且AC為b

AC/AB=BC/AC

b^2=a*(a-b)

b^2=a^2-ab

a^2-ab+(1/4)b^2=(5/4)*b^2

(a-b/2)^2=(5/4)b^2

a-b/2=（根號5/2）*b

a-b/2=(根號5)b/2

a=b/2+(根號5)b/2

a=b(根號5+1）/2

a/b=(根號5+1）/2

斐波那契數列

讓我們首先從一個數列開始，它的前面幾個數是：1、1、2、3、5、8、13、21、34、55、89、144…..這個數列的名字叫做"斐波那契數列"（也稱兔子數列），這些數被稱為"斐波那契數"。特點是即除前兩個數（數值為1）之外，每個數都是它前面兩個數之和。

經研究發現，相鄰兩個斐波那契數的比值是隨序號的增加而逐漸趨於黃金分割比的。即f(n)/f(n-1)-→0.618…。由於菲波那契數都是整數，兩個整數相除之商是有理數，所以只是逐漸逼近黃金分割比這個無理數。但是當我們繼續計算出後面更大的菲波那契數時，就會發現相鄰兩數之比確實是非常接近黃金分割比的。

一個很能說明問題的例子是五角星/正五邊形。五角星是非常美麗的，我國的國旗上就有五顆，還有不少國家的國旗也用五角星，這是為什麼？因為在五角星中可以找到的所有線段之間的長度關係都是符合黃金分割比的。正五邊形對角線連滿後出現的所有三角形，都是黃金分割三角形。

由於五角星的頂角是36度，這樣也可以得出黃金分割的數值為2Sin18 。

黃金分割點約等於0．618：1

是指分一線段為兩部分，使得原來線段的長跟較長的那部分的比為黃金分割的點。線段上有兩個這樣的點。

利用線段上的兩黃金分割點，可作出正五角星，正五邊形。

套用

生活中

有趣的是，這個數字在自然界和人們生活中到處可見：人們的肚臍是人體總長的黃金分割點，人的膝蓋是肚臍到腳跟的黃金分割點。大多數門窗的寬長之比也是0.618…；有些植莖上，兩張相鄰葉柄的夾角是137度28'，這恰好是把圓周分成1:0.618……的兩條半徑的夾角。據研究發現，這種角度對植物通風和採光效果最佳。

建築師們對數字0.618…特別偏愛，無論是古埃及的金字塔，還是巴黎的聖母院，或者是近世紀的法國艾菲爾鐵塔，都有與0.618…有關的數據。人們還發現，一些名畫、雕塑、攝影作品的主題，大多在畫面的0.618…處。藝術家們認為弦樂器的琴馬放在琴弦的0.618…處，能使琴聲更加柔和甜美。

數字0.618…更為數學家所關注，它的出現，不僅解決了許多數學難題(如：十等分、五等分圓周；求18度、36度角的正弦、餘弦值等)，而且還使優選法成為可能。優選法是一種求最最佳化問題的方法。如在煉鋼時需要加入某種化學元素來增加鋼材的強度，假設已知在每噸鋼中需加某化學元素的量在1000—2000克之間，為了求得最恰當的加入量，需要在1000克與2000克這個區間中進行試驗。通常是取區間的中點(即1500克)作試驗。然後將試驗結果分別與1000克和2000克時的實驗結果作比較，從中選取強度較高的兩點作為新的區間，再取新區間的中點做試驗，再比較端點，依次下去，直到取得最理想的結果。這種實驗法稱為對分法。但這種方法並不是最快的實驗方法，如果將實驗點取在區間的0.618處，那么實驗的次數將大大減少。這種取區間的0.618處作為試驗點的方法就是一維的優選法，也稱0.618法。實踐證明，對於一個因素的問題，用“0.618法”做16次試驗就可以完成“對分法”做2500次試驗所達到的效果。因此大畫家達·文西把0.618…稱為黃金數。

戰爭上

0.618，一個極為迷人而神秘的數字，而且它還有著一個很動聽的名字——黃金分割律，它是古希臘著名哲學家、數學家畢達哥拉斯於2500多年前發現的。古往今來，這個數字一直被後人奉為科學和美學的金科玉律。在藝術史上，幾乎所有的傑出作品都不謀而合地驗證了這一著名的黃金分割律，無論是古希臘帕特農神廟，還是中國古代的兵馬俑，它們的垂直線與水平線之間竟然完全符合1比0.618的比例。

也許，0.618在科學藝術上的表現我們已了解了很多，但是，你有沒有聽說過，0.618還與炮火連天、硝煙瀰漫、血肉橫飛的慘烈、殘酷的戰場也有著不解之緣，在軍事上也顯示出它巨大而神秘的力量？

武器裝備

在冷兵器時代，雖然人們還根本不知道黃金分割率這個概念，但人們在製造寶劍、大刀、長矛等武器時，黃金分割率的法則也早已處處體現了出來，因為按這樣的比例製造出來的兵器，用起來會更加得心應手。

當發射子彈的步槍剛剛製造出來的時候，它的槍把和槍身的長度比例很不科學合理，很不方便於抓握和瞄準。到了1918年，一個名叫阿爾文·約克的美遠征軍下士，對這種步槍進行了改造，改進後的槍型槍身和槍把的比例恰恰符合0.618的比例。

實際上，從鋒利的馬刀刃口的弧度，到子彈、炮彈、彈道飛彈沿彈道飛行的頂點；從飛機進入俯衝轟炸狀態的最佳投彈高度和角度，到坦克外殼設計時的最佳避彈坡度，我們也都能很容易地發現黃金分割率無處不在。

戰術布陣

在我國歷史上很早發生的一些戰爭中，就無不遵循著0.618的規律。春秋戰國時期，晉厲公率軍伐鄭，與援鄭之楚軍決戰於鄢陵。厲公聽從楚叛臣苗賁皇的建議，把楚之右軍作為主攻點，因此以中軍之一部進攻楚軍之左軍；以另一部進攻楚軍之中軍，集上軍、下軍、新軍及公族之卒，攻擊楚之右軍。其主要攻擊點的選擇，恰在黃金分割點上。

把黃金分割律在戰爭中體現得最為出色的軍事行動，還應首推成吉思汗所指揮的一系列戰事。仔細研究之下，從中發現了黃金分割律對戰爭勝利起的偉大作用。蒙古騎兵的戰鬥隊形與西方傳統的方陣大不相同，在它的5排制陣形中，人盔馬甲的重騎兵和快捷靈動輕騎兵的比例為2:3，這又是一個黃金分割！

馬其頓與波斯的阿貝拉之戰，是歐洲人將0.618用於戰爭中的一個比較成功的範例。在這次戰役中，馬其頓的亞歷山大大帝把他的軍隊的攻擊點，選在了波斯大流士國王的軍隊的左翼和中央結合部。巧的是，這個部位正好也是整個戰線的“黃金點”，所以儘管波斯大軍多於亞歷山大的兵馬數十倍，但憑藉自己的戰略智慧，亞歷山大把波斯大軍打得潰不成軍。這一戰爭的深刻影響直到今天仍清晰可見， 在海灣戰爭中，多國部隊就是採用了類似的布陣法打敗了伊拉克軍隊。

兩支部隊交戰，如果其中之一的兵力、兵器損失了1/3以上，就難以再同對方交戰下去。正因為如此，在現代高技術戰爭中，有高技術武器裝備的軍事大國都採取長時間空中打擊的辦法，先徹底摧毀對方1/3以上的兵力、武器，爾後再展開地面進攻。讓我們以海灣戰爭為例。戰前，據軍事專家估計，如果共和國衛隊的裝備和人員，經空中轟炸損失達到或超過30%，就將基本喪失戰鬥力。

戰略戰役

0.618不僅在武器和一時一地的戰場布陣上體現出來，而且在區域廣闊、時間跨度長的巨觀的戰爭中，也無不得到充分地展現。

一代梟雄的的拿破崙大帝可能怎么也不會想到，他的命運會與0.618緊緊地聯繫在一起。1812年6月，正是莫斯科一年中氣候最為涼爽宜人的夏季，在未能消滅俄軍有生力量的博羅金諾戰役後，拿破崙於此時率領著他的大軍進入了莫斯科。1941年6月22日，納粹德國啟動了針對蘇聯的“巴巴羅薩”計畫，實行閃電戰，在極短的時間裡，就迅速占領了的蘇聯廣袤的領土，並繼續向該國的縱深推進。在長達兩年多的時間裡，德軍一直保持著進攻的勢頭，直到1943年8月，“巴巴羅薩”行動結束，德軍從此轉入守勢，再也沒能力對蘇軍發起一次可以稱之為戰役行動的進攻。被所有戰爭史學家公認為蘇聯衛國戰爭轉折點的史達林格勒戰役，就發生在戰爭爆發後的第17個月，正是德軍由盛而衰的26個月時間軸線的黃金分割點。

其它

我們常常聽說有“黃金分割”這個詞，“黃金分割”當然不是指的怎樣分割黃金，這是一個比喻的說法，就是說分割的比例像黃金一樣珍貴。那么這個比例是多少呢？是0.618。人們把這個比例的分割點，叫做黃金分割點，把0.618叫做黃金數。並且人們認為如果符合這一比例的話，就會顯得更美、更好看、更協調、更美麗。在生活中，對“黃金分割”有著很多的套用。

最完美的人體：肚臍到腳底的距離/頭頂到腳底的距離=0.618

最漂亮的臉龐：眉毛到脖子的距離/頭頂到脖子的距離=0.618