基本介紹
- 中文名:正十邊形
- 外文名:regular decagon
- 學科:數學
- 周長:10a
- 內角和:1440°
- 相關名詞:正八邊形
簡介,對稱性,周長求法,內角和,尺規作圖,圓內接正十邊形面積,
簡介
正十邊形的每個內角是144°,每個外角是36°。正十邊形既是軸對稱圖形,又是中心對稱圖形。它的中心角度數為36°,根據正多邊形邊長計算公式an=2Rsin(180°/n)可得知其邊長與其外接圓半徑比為﹙√5-1)/2=2sin18°符合黃金分割比,所以正十邊形是唯一符合黃金分割比的正多邊形。

對稱性
周長求法
設正十邊形的邊長是a,則它的周長是10a。
內角和
正十邊形的內角和為(10-2)×180°
同理n邊形的內角和為 從n邊形的一個頂點出發,可以引n-3條對角線,他們將n邊形分成n-2個三角形,n邊形的內角和等於180°×﹙n-2﹚
尺規作圖
用尺規可以做出正十邊形,方法如下。
1、作圓O,半徑OA;
2、過點A作OA的垂線段AB,使AB=1/2OA;
3、連結OB.在OB上截取BC=AB;
4、以OC為半徑,A為起點,在圓O上依次截取相等的弧AD=DE=EF=FG=GH……=LA;
依次連結成一個正十邊形。
圓內接正十邊形面積
已知圓O的半徑為r,計算其內接正十邊形的面積:
為了方便,畫出簡單的示意圖(正十邊形的半徑把正十邊形分成十個全等的等腰三角形,示意圖只畫了其中的一個三角形,如圖

因為∠ ,所以
,所以 是頂角為
是頂角為 的等腰三角形。
的等腰三角形。



由等腰三角形的結論, ,
,

作0C丄AB,垂足為C,則 ,在直角三角形OAC中,由勾股定理
,在直角三角形OAC中,由勾股定理 。
。


所以 。
。

所以所求正十邊形的面積為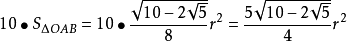 。
。