基本介紹
- 中文名:鷹鴿博弈
- 外文名:Hawk-dove game
- 學科領域:博弈論、生物進化
- 提出者:約翰·史密斯
介紹
純策略均衡
混合策略均衡
貝葉斯博弈
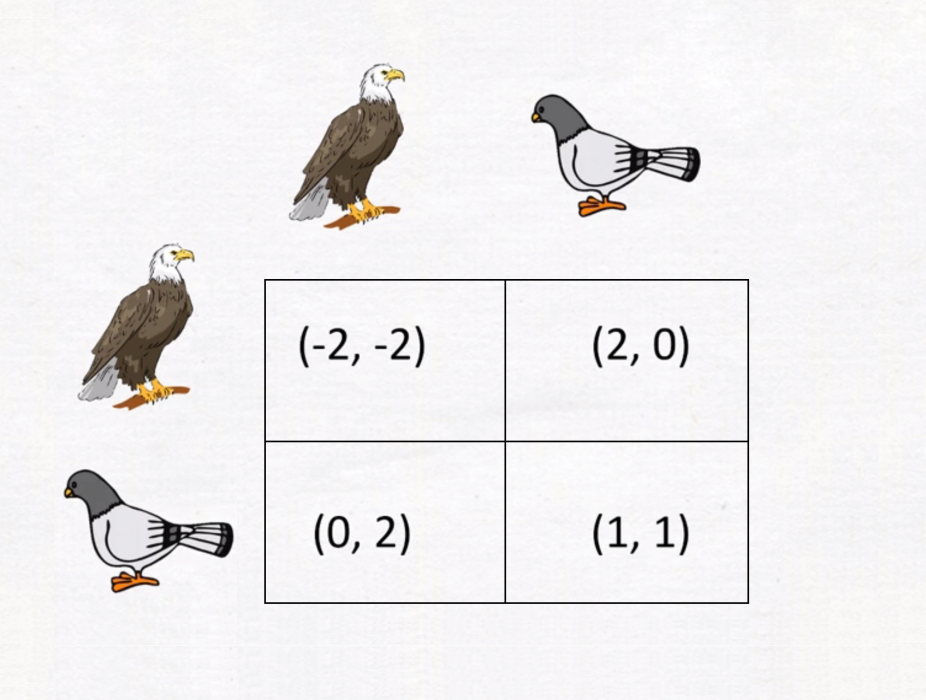
鷹-鷹 | 奪食 | 逃走 | 鴿-鴿 | 奪食 | 逃走 | 鷹-鴿 | 奪食 | 逃走 | ||
奪食 | -2,-2 | 2,-1 | 奪食 | 1,1 | 2,0 | 奪食 | 2,-2 | 2,0 | ||
逃走 | -1,2 | -1,-1 | 逃走 | 0,2 | 0,0 | 逃走 | -1,2 | -1,0 |

鷹-鷹 | 奪食 | 逃走 | 鴿-鴿 | 奪食 | 逃走 | 鷹-鴿 | 奪食 | 逃走 | ||
奪食 | -2,-2 | 2,-1 | 奪食 | 1,1 | 2,0 | 奪食 | 2,-2 | 2,0 | ||
逃走 | -1,2 | -1,-1 | 逃走 | 0,2 | 0,0 | 逃走 | -1,2 | -1,0 |

鷹鴿博弈是英國生物學家約翰·梅納德·史密斯提出的一個博弈論模型,用來解釋自然界中的鷹與鴿子兩個物種的進化與共存現象。該模型的兩個純策略均衡類似於膽小鬼博弈...
表1: 鷹鴿貝葉斯博弈的三種遭遇下的支付矩陣按照Harsanyi 變換的思路,一隻鷹決定自己的奪食機率 a 時會考慮下表的四種情況。若選擇奪食,對方是鷹的機率為 0.5,...
生存博弈目錄 編輯 生存博弈 第1章 生存在博弈中囚徒困境:兩難境地的抉擇鷹鴿博弈:強硬與溫和的演進定局樓君臣鬥智:局內局外皆博弈
第十二章 分蛋糕博弈:神奇的生活經濟學時間就是金錢特殊的威脅方式:邊緣策略偷梁換柱的“等價法”主動設計博弈局勢第十三章 鷹鴿博弈:進化中的“頑固因子”...
其代表作《演化與博弈論》是演化博弈論領域的經典著作。演化與博弈論目錄 編輯 譯叢總序前言第一章 導論第二章 基本模型一、 鷹鴿博弈...
10.3隨大流博弈的演化均衡點與演化穩定均衡點10.4趨中博弈——鷹鴿博弈(HawkDoveGame)的演化穩定點10.5懶人博弈的演化穩定點與演化均衡點 [1] ...
比例博弈 再看鷹鴿博弈 供給、需求和試算法 凱恩斯經濟學和協調問題 假設的利弊 小結 練習與討論 第三部分 博弈的合作解 第12章 合作博弈的要素 腳踏車交易 可信...
第十三章鷹鴿博弈:讓事業進入良性循環 1.鷹鴿博弈:強硬者與溫和者的博弈對決/230 2.遵守社會慣例:它有著一定的穩定性/231 3.“隨大流”也有著理性的一面...
第八節鷹鴿博弈:演化博弈分析方式 策略篇 第五章理論策略 第一節選數博弈:優勢策略與劣勢策略 第二節田忌賽馬:零和博弈與變和博弈 第三節熟人社會:一次...
鷹鴿博弈:讓事業進入良性循環慣例是社會的紐帶/258隨大流的理性一面/259成與敗都會自我強化/262勝出的未必是好的/265改革就要立竿見影/266...
鷹鴿博弈:戰爭與和平賭徒博弈:在人生的賭局中別犯賭徒的錯膽小鬼博弈:狹路相逢誰獲勝分蛋糕博弈:二一添作五的結局第三篇 典型的博弈策略常識...
第6章 酒吧博弈:混沌狀態的選擇第7章 獵鹿博弈:大家好才在是真的好第8章 蜈蚣博弈:直覺與理性的背叛第9章 鷹鴿博弈:強硬與溫和的演講...
第六章:分蛋糕博弈——討價還價的策略第七章:以牙還牙——有一種智慧叫寬恕第八章:鷹鴿博弈——路徑依賴法則新解第九章:蜈蚣博弈——從後往前的推理...
生存博弈:現實社會中的策略競爭圖書目錄 編輯 第1章 生存在博弈中囚徒困境:兩難境地的抉擇鷹鴿博弈:強硬與溫和的演進定局樓君臣鬥智:局內局外皆博弈...
第十一章 蜈蚣博弈:學會以結果為導向思考問題 強盜分金模型 倒後推理的威力 人生的倒後推理 蜈蚣博弈悖論 第十二章 鷹鴿博弈:強硬與溫和的演繹 ESS穩定...
進入社會的49堂博弈課圖書目錄 編輯 第一章顛覆:進入社會,換一套思維來活第1堂課 鷹鴿博弈:偃旗息鼓的智慧第2堂課 智豬博弈:既做聰明人,又出傻力氣...
第十章 進化博弈 第一節 進化博弈的基本思想 第二節 囚徒困境 第三節 膽小鬼博弈 第四節 物種間的相互作用 第五節 鷹鴿博弈 第六節 某些一般性理論 第七節...
第十二章 分蛋糕博弈:神奇的生活經濟學 時間就是金錢 特殊的威脅方式:邊緣策略 偷梁換柱的“等價法” 主動設計博弈局勢 第十三章 鷹鴿博弈:進化中的“...
王春永鷹鴿博弈 這個博弈很多人等同於鬥雞博弈。不過,鬥雞是兩個兼具侵略性的個體,鷹鴿卻是兩個不同群體的博弈,一個和平,一個侵略。在只有鴿子一個苞穀場里,...
五、在共同記憶中形成重複性協調博弈的解六、“無理由”的理由七、信號與均衡的調整第3章鷹鴿博弈:避免更糟一、鷹還是鴿?二、謝林的方法:邊緣策略...
