高等教學主要包括函式與極限分為、導數與微分、導數的套用、不定積分、定積分及其套用、空間解析幾何、多元函式的微分學、多元函式積分學、常微分方程、無窮級數。
基本介紹
- 中文名:高等教學
- 對應:函式與極限
- 對象:導數與微分
- 屬性:變數。
簡介
分類
主要包括
導數的概念
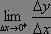

高等教學主要包括函式與極限分為、導數與微分、導數的套用、不定積分、定積分及其套用、空間解析幾何、多元函式的微分學、多元函式積分學、常微分方程、無窮級數。
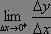
高等教育是在完成中等教育的基礎上進行的專業教育和職業教育,是培養高級專門人才和職業人員的主要社會活動。高等教育是教育系統中互相關聯的各個重要組成部分之一。它...
高等教學主要包括函式與極限分為、導數與微分、導數的套用、不定積分、定積分及其套用、空間解析幾何、多元函式的微分學、多元函式積分學、常微分方程、無窮級數。...
普通高等教育指主要招收高中畢業生進行全日制學習的專業教育。普通教育是和成人教育相對應的概念,普通教育的對象主要是處於成長階段的青少年,採取全日制教學形式。普通...
高等教育部是指主管高等教育的國家教育行政機構。在中華人民共和國,於 1952 年 11 月成立。宗旨:統一與集中管理高等學校,加強對它們的改革和整頓,設有辦公廳、...
高等職業教育是我國教育的重要組成部分,包括高等專科教育、高等職業本科教育、研究生層次職業教育和成人高等教育(以下簡稱高職教育),是教育發展中的一個類型,肩負著為...
高等院校指按照國家規定的設定標準和審批程式批准舉辦,通過普通高等學校、成人高等學校招生全國統一考試,招收普通高中畢業生為主要培養對象,實施高等教育的全日制大學、...
成人高等教育屬國民教育系列,是高等教育的重要組成部分,國家承認學歷,參加全國招生統一考試,各省、自治區統一組織錄取。成人高等學歷教育分為三種:專科起點升本科(簡稱...
高等學校泛指對公民進行高等教育的學校,是大學、學院、獨立學院、高等職業技術大學、高等職業技術學院、高等專科學校的統稱,與大學詞義相近。中國大陸高等教育系統擁有雙...
高等學校本科教學工作水平評估,簡稱:本科教學工作水平評估,是指普通高等學校本科教學工作水平評估,以《中華人民共和國高等教育法》為依據,貫徹“以評促改,以評促建,...
高等教育學是一門以高等教育的運行形態和發展基本規律為研究對象的具有綜合性、理論性和套用性的教育科學。...
高等教育機構,泛指實施高等教育的學校和具有研究生招生教育資格的科研院所,指提供教學和研究條件和授權頒發學位的高等教育組織,包括大學、學院、高等職業技術學院、高等...
摘要 本書在深入研究德國工程技術教育模式及其特色的基礎上,重點探討了工程技術教育實踐教學體系的建立問題,通過對比分析中、德兩國在工程技術教育領域中存在的差異,...
高等學校教學指導委員會是教育部領導的專家組織。自成立以來,在教育部和有關部門的領導下積極開展工作,在課程和教材建設、教學改革、巨觀戰略研究、教育質量監控、...
高等教育大學生教育階段分為三種形式:大學本科(大本)、研究生(包括碩士研究生和博士研究生)和大學專科(大專)。通常情況下,接受高等教育的學生在正常畢業後通常頒發...
中華人民共和國高等教育法,是為了發展高等教育事業,實施科教興國戰略,促進社會主義物質文明和精神文明建設, 根據憲法和教育法,制定的法規。《高等教育法》由中華人民...
《高等醫學教育學》是2004年人民軍醫出版社出版的圖書,作者是蘇博,劉鑒汶。... 《高等醫學教育學》是2004年人民軍醫出版社出版的圖書,作者是蘇博,劉鑒汶。...
高等學歷教育是指受教育者經過國家教育考試, 進入實施高等學歷教育的高等學校或者 其他高等教育機構。...
《高等理科教育》創刊於1993年,是由中華人民共和國教育部主管,中國高等教育學會理科教育專業委員會、蘭州大學主辦的以高等理科教育和高等教育為研究對象的學術性刊物。...
高等學校教學計畫是指高等學校各系科、專業培養學生的方案。在中國,一般包括下列各項規定:培養目標、修業年限、學生畢業應修滿的總學時或總學分、課程設定(公共課...
高等教育是中等教育之後所實施的各種專門教育。在我國,高等教育包括全日制高等教育和成人高等教育兩個類型,後者屬於成人教育範疇。 中國高等教育分為專科生、本科生、...
《高等藝術教育教學研究》是2012年出版的圖書,作者是劉大力。... 《高等藝術教育教學研究》是2012年出版的圖書,作者是劉大力。作者 劉大力 ISBN 9787560745244 ...
《高等教育十論》是1992年華東師範大學出版社出版的圖書。... 高等教育十論編輯 鎖定 討論 《高等教育十論》是1992年華東師範大學出版社出版的圖書。...
《教育部高等學校教學指導委員會章程》是教育部辦公廳2018年12月20日下發的檔案;本章程共七章二十一條,公布之日起施行。...
高等教育學是在教育學專業的基礎上設立的,是培養從事高等教育領域的教學、科研和管理工作的高層次專門人才的新學科專業。南昌大學高等教育學專業的研究方向有:地方...
高等職業技術教育是屬於第三級教育層次的職業教育和技術教育。包括就業前的職業技術教育和從業後的有關繼續教育。如美國技術學院和社區學院的部分教學計畫,日本高等專門...
《中國高等教育》由中華人民共和國教育部創辦並直接主管,是全國高等教育導向性、綜合性理論刊物。其前身是創刊於1965年,復刊於1982年的《高教戰線》,1986年7月...
《高等技術教育學》是2011-年上海交通大學出版社出版的圖書,作者是夏建國 。... 夏建國院長主編的《高等技術教育學》論述了高等技術教育的相關問題,詮釋了高等技術...
大學(University),是一種功能獨特的文化機構,是與社會的經濟和政治機構既相互關聯又鼎足而立的傳承、研究、融合和創新高深學術的高等學府。它不僅是人類文化發展到...
《高等學校教學原理與方法》是1970-1出版的圖書,作者是潘懋元 編。... 《高等學校教學原理與方法》一書,是全國教育科學研究“七五”規劃國家級重點項目的研究成果...
