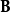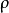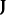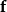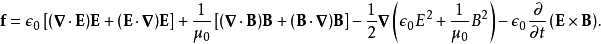馬克士威應力張量

在電磁學里，馬克士威應力張量，即麥克斯韋應力張量(Maxwell stress tensor)是描述電磁場帶有之應力的二階張量。麥克斯韋應力張量可以表現出電場力、磁場力和機械動量之間的相互作用。對於簡單的狀況，例如一個點電荷自由地移動於均勻磁場，套用洛倫茲力定律，就可以很容易地計算出點電荷所感受的作用力。但是，當遇到稍微複雜一點的狀況時，這很普通的程式會變得非常困難，方程洋洋灑灑地一行又一行的延續。因此，物理學家通常會聚集很多項目於麥克斯韋應力張量內，然後使用張量數學來解析問題。

基本介紹

• 中文名：馬克士威應力張量
• 外文名：Maxwell stress tensor
• 範圍：電磁學里
• 定義：二階張量
• 別稱：麥克斯韋應力張量

導引

先列出麥克斯韋方程組，高斯定律： 高斯磁定律： 法拉第感應定律： 麥克斯韋-安培定律：

其中， 是電場， 是磁場， 是電荷密度， 是電流密度， 是電常數， 是磁常數。

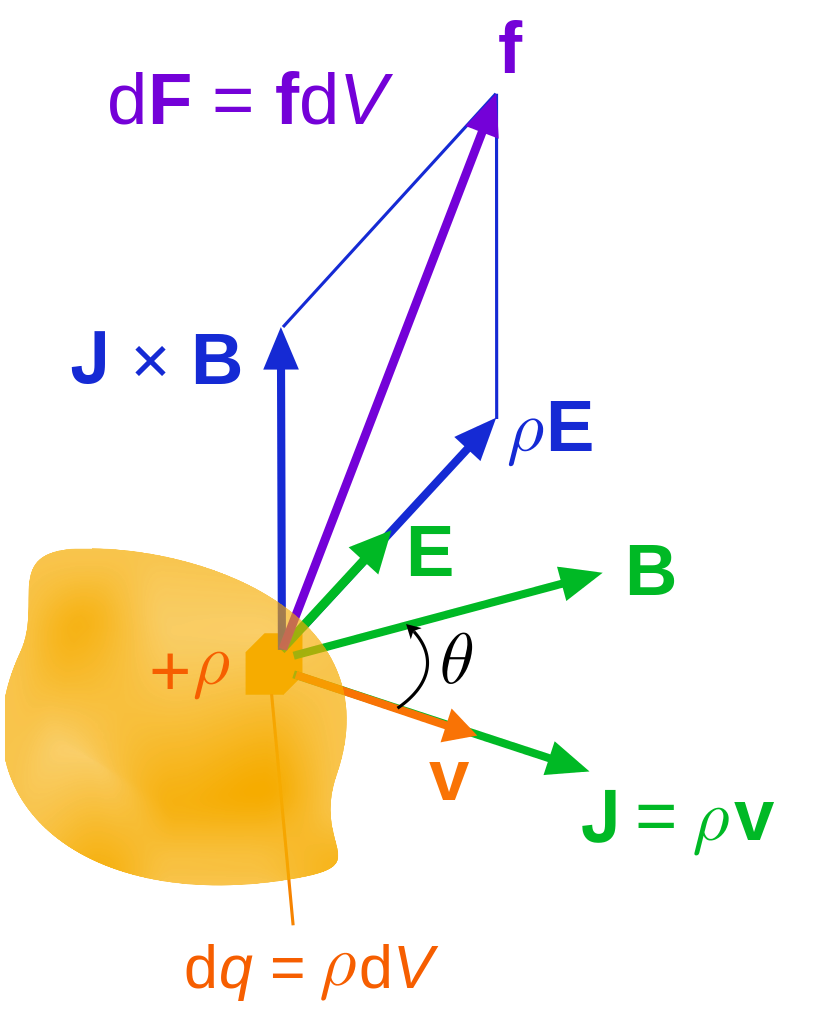
從洛倫茲力定律開始，一個電荷分布所感受到的單位體積的作用力 是

套用高斯定律和麥克斯韋-安培定律，把電荷密度和電流密度替換掉，只讓電場和磁場出現於方程：

套用乘積法則和法拉第感應定律：

為了使 的項目 的項目能夠相互對稱，加入一個 項目：

套用矢量恆等式，對於任意矢量 ：

將 的方程內的旋度項目除去：

這方程最右邊項目涉及了坡印亭矢量：

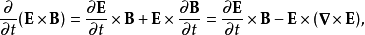
設定麥克斯韋應力張量 （以英文字母上面加兩隻箭矢符號來標記二階張量）：

其中， 是克羅內克函式。

定義一個矢量 與麥克斯韋應力張量 的內積為

那么，一個電荷分布所感受到的單位體積的作用力 是

麥克斯韋應力張量的性質

麥克斯韋應力張量是一個對稱張量，表達為

麥克斯韋應力張量的單位是牛頓/米。麥克斯韋應力張量的 ij 元素詮釋為，朝著 i-軸方向，施加於 j-軸的垂直平面，單位面積的作用力；對角元素代表負壓力，非對角元素代表剪應力。對角元素給出張力（拖拉力）作用於其對應軸的垂直面微分元素。不同於理想氣體因為壓力而施加的作用力，在電磁場內的一個面元素也會感受到方向不垂直於其面的剪應力。這是由非對角元素給出的。

動量守恆定律

在一個體積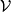 內的電荷，所感受到的總作用力 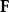是

套用散度定理，可以得到

其中， 是體積 的閉合表面。

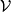
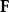
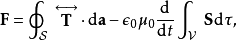
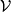
根據牛頓第二定律，

其中， 是動量。

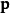
所以，電荷的動量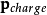 可以表達為

其中， 是儲存於電磁場的動量（坡印亭矢量是由電場和磁場組成的一個複合矢量）。

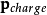
稍加編排，可以得到動量守恆定律的積分方程：

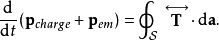
動量守恆定律闡明，一個體積的總動量（電荷的動量加上電磁場的動量）的增加速率等於每秒鐘流入閉合表面的動量。負的麥克斯韋應力張量 是一個動量通量密度。

動量守恆定律也能以微分形式表達為

其中， 是電荷的動量密度， 是電磁場的動量密度。

相關條目

• 電磁能量密度
  
• 坡印亭矢量
  
• 電磁應力-能量張量
  
• 電磁場的數學表述