順序符號(sign of order)是常用的數學符號之一,指用來確定運算順序的符號。常用的順序符號有:—、( )、[ ]、{ },他們分別稱為括線、小括弧(或圓括弧)、中括弧(或方括弧)、大括弧(或花括弧)。在計算過程中確定的順序是:先算括線,次算小括弧,再次中括弧,最後算大括弧。
基本介紹
- 中文名:順序符號
- 外文名:sign of order
- 所屬學科:數學
- 所屬問題:算術
- 簡介:用來確定運算順序的符號
基本介紹
常用順序符號簡介
小括弧
中括弧
大括弧



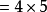
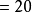
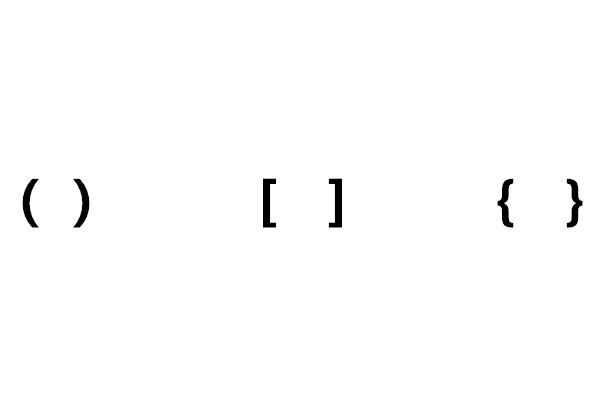
順序符號(sign of order)是常用的數學符號之一,指用來確定運算順序的符號。常用的順序符號有:—、( )、[ ]、{ },他們分別稱為括線、小括弧(或圓括弧)、中括弧(或方括弧)、大括弧(或花括弧)。在計算過程中確定的順序是:先算括線,次算小括弧,再次中括弧,最後算大括弧。



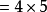
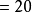
順序符號(sign of order)是常用的數學符號之一,指用來確定運算順序的符號。常用的順序符號有:—、( )、[ ]、{ },他們分別稱為括線、小括弧(或圓括弧)、中...
流程圖符號是專門用來畫圖的,其中有流程圖,裡面有符號的解釋。不管什麼符號,都需要給它定義,定義行為是由制定人予以完成的,要完成這項工作不應該先定義符號代表什麼...
關係符號(relational symbols)是表示數與數、式與式之間的某種關係的特定記號,這種關係符號有大於號、小於號、等於號、約等於號等。...
《標點符號用法》是1995年中國標準出版社出版的圖書,作者是國家語委語言文字套用研究所。該書是一部國家標準,規定了標點符號的名稱、形式和用法,對漢語書寫規範有...
漢語注音符號(Chinese zhuyin),簡稱注音符號,又稱注音字母,是為漢語漢字注音而設定的符號。以章太炎的記音字母作藍本,1913年由中國讀音統一會制定,1918年北洋政府...
C語言運算符號指的是運算符號。C語言中的符號分為10類:算術運算符、關係運算符、邏輯運算符、位操作運算符、賦值運算符、條件運算符、逗號運算符、指針運算符、求...
在加減法中,運算順序是可以改變,例如:3-8+5,可以改變為3+5-8,將5移到-8的前面,在移動的時候要帶著前面的運算符號一起,改變運算順序無非為了運算更簡單 [3...
順序點,也稱作序列點,是電腦程式中一些執行點,在該點處之前的求值的所有的副作用已經發生,在它之後的求值的所有副作用仍未開始。在C與C++程式設計語言中,表達式...
符號方法是通過估計符號(常常是字元)的機率值來壓縮文本,它在同一時間只對一個符號編碼,如摩斯碼,對最可能出現的符號使用較短的碼字。符號方法屬於外部壓縮方法,...
項目符號是放在文本(如列表中的項目)前以添加強調效果的點或其他符號。...... Word 會自動按順序處於第一級別的每一行的開頭插入數字。若要將多級符號項目移動到所...
順序圖是將互動關係表示為一個二維圖。縱向是時間軸,時間沿豎線向下延伸。橫向軸代表了在協作中各獨立對象的類元角色。類元角色用生命線表示。當對象存在時,角色...
分類號碼是代表各級類目的標記,是分類表中類目的代碼,故又稱標記符號。標記符號是類目的代號,具有固定類目位置的作用,可以確定各級類目的先後次序,還可以表示類目之間...
位元組順序是指占記憶體多於一個位元組類型的數據在記憶體中的存放順序,通常有小端、大端兩種位元組順序。小端位元組序指低位元組數據存放在記憶體低地址處,高位元組數據存放在記憶體高...
根據符號的來源和目的將其分為兩類。“某些符號是為了意指而製造出來的客體(OBJECT),而另一些符號是為了使用功能而製造出來的客體。” 而建築符號,就是後一種,...
符號表征階段是布魯納認知發展理論術語。兒童認知發展的第三階段,也是最後階段。在此階段,兒童不必依據動作或表象的幫助而依據符號、語言文字即可從事抽象思維,從彼此...
首先隨意製造一個3個3×3的Polybius方格替代密碼,包括26個英文字母和一個符號。然後寫出要加密的訊息的三維坐標。訊息和坐標四個一列排起,再順序取橫行的數字,三...
數字符號(英語:numero sign或numero symbol),也可記作為№、Nº、No或no,法語“numéro”的縮寫。在英語中,“No.”經常被用來取代“number”。字型排印學中...
中括弧(bracket),又稱方括弧,符號“[ ]”,常成對使用。是一種記號,用以連線需一起考慮的、相等的或成對的單詞或項目,或者圍起從中只選取一個的那些項目。....
文獻分類法類目的標記符號與標記制度。它是現代文獻分類法的重要組成部分,具有指示類目位置,表示類目排列次序及其相互關係的作用。...
圖例是集中於地圖一角或一側的地圖上各種符號和顏色所代表內容與指標的說明,有助於更好的認識地圖。它具有雙重任務,在編圖時作為圖解表示地圖內容的準繩,用圖時...
