基本介紹
- 中文名:非退化矩陣
- 外文名:non-degenerate matrix
- 所屬學科:數學
- 別名:非(奇)異矩陣,滿秩矩陣等
- 特點:n階方陣A的行列式|A|≠0
- 充要條件:A是非退化充要條件為A是可逆矩陣
- 類型:數學術語
基本介紹

相關結論





















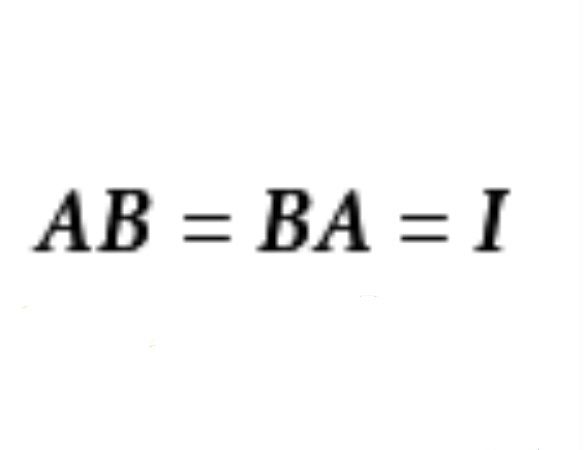






















非退化矩陣(non-degenerate matrix)又稱“非異矩陣(non-singular matrix) ”、“滿秩矩陣”,若n階矩陣A的行列式|A|≠0,則稱A為一個非退化矩陣,若|A|=0,則稱A為“退化矩陣...
完全不確定Hamburger矩陣矩量問題的有限階解 對矩陣值函式的Nevanlinna—Pick插值問題與冪矩量問題(Ⅱ)一般有理插值問題及其與Nevanlinna—Pick插值和冪矩量問題的聯繫 對矩陣值函式的Nevanlinna—Pick插值問題與冪矩量問題 非退化與退化...
數域P上n*n矩陣A,B稱為契約的,如果有數域P上可逆的n*n矩陣C,使B=C'AC.矩陣契約變換是在矩陣左右兩邊分別乘C'和C,其中C為非退化矩陣.契約變換是在分析二次型的化簡過程中產生的,二次型的矩陣通過契約變換化為形式上比較簡單...
對稱是指gμν=gνμ 其中μ、ν為矢量空間V中任意矢量,非退化是指若且唯若μ或ν為矢量空間中零矢量時gμν=0。註:若g為非退化,則他在V的任一基底{eμ}的分量gμν≡g(eμ,ev)排成的矩陣為非退化矩陣(行列式非零...
若正交旋轉後的公因子仍然沒有明顯的實際意義,亦可作方差極大的斜交旋轉,選擇適當的非退化矩陣P(P非正交陣),使AP的總方差達最大的變換稱為方差極大的斜交旋轉,變換矩陣P是一般的非奇異矩陣,故具有更大的選擇性。具體旋轉方法與...
對於所有g∈G和某個非退化矩陣M.對於每一個群,至少有一個表示:映射群的每一個元素到單位矩陣。則上面所有的公理都滿足.但它不是一個非常有價值的表示,被稱作群的平凡表示(trivial representation).如果群的每一個不同的元素都由...
非退化:如果 ω(u, v) = 0 對所有 v ∈ V 成立,那么 u = 0 。取定一組基,ω 能表示為一個矩陣。以上兩個條件表明這個矩陣必須是斜對稱非奇異矩陣。這不同於下面將介紹的辛矩陣,辛矩陣表示空間的一個辛變換。如果 V ...
1.3.3 矩陣的行列式 9 1.3.4 矩陣的秩 9 1.3.5 非退化矩陣 10 1.4 可逆矩陣的判定與計算 10 1.4.1 可逆矩陣的概念 10 1.4.2 可逆矩陣的性質 10 1.4.3 矩陣可逆的判定和求法 10 1.4.4 與可逆矩陣相乘不改變原...
2.1 矩陣及基本運算 2.1.1 定義 2.1.2 運算法則 2.2 逆矩陣 2.2.1 非退化矩陣 2.2.2 用行初等變換求逆陣 2.2.3 套用舉例(投入產出分析)習題二 第三章 線性代數方程組的相容性 3.1 矩陣的秩 3.1.1...
非退化:如果 ω(u,v) = 0 對所有v∈V成立,那么u= 0 。取定一組基,ω 能表示為一個矩陣。以上兩個條件表明這個矩陣必須是斜對稱非奇異矩陣。這不同於下面將介紹的辛矩陣,辛矩陣表示空間的一個辛變換。如果V是有限維的那么...
稱為埃爾米特二次型,A 稱為 Q 的矩陣,其中 因而 a 都是實數,即 是埃爾米特矩陣。性質 作非退化線性代換 X=TY,其中 所得到的二次型的矩陣 B 與 矩陣 A 的關係為 ,對埃爾米特二次型也可以與二次型一樣地定義秩、等價...
看成線性替換,那么它就是非退化的,因為 性質 1.因為二次型和它的矩陣是相互唯一決定的,令 故線性替換 可以寫成 2.經過一個非退化的線性替換,二次型還是變成二次型。具體地:設 是一個二次型,作非退化線性替換 我們可以得到...
取定域F上一個n×n對稱或反對稱矩陣M。 令g={X∈g{(n,F)| tXM+MX =0}(X表示X的轉置), 則g是g{(n,F)的子代數。現設F是複數域,M是一個非退化對稱矩陣,於是M與以下兩個矩陣之一契約:當n=2l+1時,有:當n=2l...
),則為非退化,如果c = 0則為退化(即 )。f的非退化臨界點b的指數是H的切線空間與M的最大子空間的尺寸,其中海森矩陣是負定的。 這對應於直觀的概念,即索引是f減少的方向數。 關鍵點的簡併性和指數與所使用的局部坐標系...
。寫成矩陣,設這個形式用矩陣 Φ 表示,這便是說 M *ΦM = Φ。就像實數上的對稱形式,埃爾米特形式由符號確定,所有都是酉契約於對角線上 p 個元素為 1,q 個 - 1 的對角矩陣。非退化假設等價於 p + q = n。在一組...
,en},當基域的特徵不為2時,對稱雙線性型B的矩陣S=(B(ei,ej))滿足S′=S,即為對稱矩陣。概念 正交幾何是一種向量空間的幾何,即關於非退化對稱雙線性型的向量空間的研究。這裡的對稱雙線性型B是指對任意向量x,y有B(x,y...
稱V為非退化對稱(反對稱)或滿秩對稱(反對稱)雙線性度量空間.以上各種度量空間,簡稱度量空間.在度量空間內抓a,戶常用內積((a,夕)表示.對V中任意m個向量al}a2}...}am,由內積(a; , a;)為(i,j)元素組成的m階矩陣((a;,...
,xn)總可以經過實係數的非退化線性替換X=CY化為平方和的形式,稱作實二次型f(x1,x2,…,xn)的規範形,其中平方項的個數r等於二次型的秩.任一實二次型的規範形是唯一的,即若實二次型f(x1,x2,…,xn)經過實係數非退化...
在複數域的特殊情形,全體n×n酉方陣在矩陣乘法下構成的群稱為n次酉群,記為U(n)。一般地,設K是帶有對合J:a→a-的體,V是K上n維列向量空間,f(x,y)=x-Hy是V上非退化厄米特型或反厄米特型,這裡H∈GLₙ(K)且=ε...
