非緊性測度(measures of noncompactness)是抽象空間微分方程理論的基本概念。
基本介紹
- 中文名:非緊性測度
- 外文名:measures of noncompactness
- 適用範圍:數理科學
簡介
性質
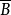


非緊性測度(measures of noncompactness)是抽象空間微分方程理論的基本概念。
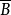


非緊性測度(measures of noncompactness)是抽象空間微分方程理論的基本概念。...... 非緊性測度(measures of noncompactness)是抽象空間微分方程理論的基本概念。...
設X,Y為完備度量空間,f:X→Y連續有界,ψx與ψγ分別為X與Y上的非緊性測度。若對於X中每個有界的非相對緊集A,均有ψγ(f(A))<ψγ(A),則稱f為(...
如果對x中集M,定義M的非緊性測度為式,那么全連續運算元T的定義又可以改述為:對一切有界集M,滿足v(TM)=0的運算元。x 上的有限秩運算元(即值域是有限維的有界...
7.3.3非緊性測度 7.3.4集壓縮映射的不動點 7.3.5Kakutani不動點定理 7.3.6套用:代數學基本定理 7.3.7套用:不變子空間 7.3.8套用:對策論基本定理 ...
第一章 預備知識1.1 非緊性測度1.2 中值定理與比較定理1.3 半內積1.4 附註第二章 Cauchy問題的存在惟一性2.1 近似解與解的關係2.2 解的存在惟一性...
7.3.3 非緊性測度7.3.4 集壓縮映射的不動點7.3.5 Kakutani不動點定理7.3.6 套用:代數學基本定理7.3.7 套用:不變子空間7.3.8 套用:對策論基本定理...
集壓縮映射是在集合的非緊性測度意義下壓縮的映射。(嚴格)集壓縮映射必是凝聚的。...... 集壓縮映射是在集合的非緊性測度意義下壓縮的映射。(嚴格)集壓縮映射必...
7.3.3 非緊性測度 7.3.4 集壓縮映射的不動點 7.3.5 Kakutani 不動點定理 7.3.6 套用:代數學基本定理 7.3.7 套用:不變子空間 7.3.8 套用:對策...
