基本介紹
- 中文名:非標準模型
- 外文名:non standard model
- 適用範圍:數理科學
定義













模型


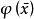

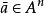



























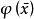

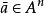











非標準模型簡單地說就是與自然模型(或稱標準模型、期望模型)不同構的模型。非標準模型雖然不是人們所期望的,但是它們有時卻有著非常重要的套用。開發理論的非標準...
非標準算術模型(nonstandard model of peano arithmetic)是皮亞諾算術理論的一種模型,指與自然數模型N初等等價,但不同構的模型。自然數集合的皮亞諾公理(Peano ...
在粒子物理學裡,標準模型(英語:Standard Model, SM)是一套描述強力、弱力及電磁力這三種基本力及組成所有物質的基本粒子的理論。它隸屬量子場論的範疇,並與量子...
非標準全域是標準全域的非標準模型,它是另一個超結構的子集。非標準全域也可用公理方法建立。...
非標準微積分(nonstandard calculus)是在分析的非標準模型中展開的微積分。...... 非標準微積分(nonstandard calculus)是在分析的非標準模型中展開的微積分。...
標準模型理論(簡稱SM)是一套描述強力、弱力及電磁力這三種基本力及組成所有物質的基本粒子的理論,以楊-米爾斯方程為核心,又稱為規範對稱場論。標準模型理論隸屬...
B模型(B-model)也叫作B擴大。B模型是一種特殊的非標準模型。...... B模型亦稱B擴大,是一種特殊的非標準模型。設K是一個句子集合,T是在K中出現的一切常項所...
非線性模型(nonlinear model)指反映自變數與依變數間非線性關係的數學表達式,它相對於線性模型而言,其依變數與自變數間不能在坐標空間表示為線性對應關係。...
非參數模型是指系統的數學模型中非顯式地包含可估參數。例如,系統的頻率回響、脈衝回響、階躍回響等都是非參數模型。...
非標準實數(non-standard real number)見“標準模型”。 ...... 非標準實數(non-standard real number)見“標準模型”。 [1] 參考資料 1. 金炳華等編.哲學大...
本書作者在國家自然科學基金的資助下,用超有限經濟模型研究“雙無限”經濟問題,取得了可喜結果。中文名 非標準經濟學 引入者 布朗 羅賓遜 引入時間 1974年 ...
粒子物理標準模型(particle physics, standard model of)是關於已知物質的微觀最基本單元——輕子和夸克,最基本相互作用(三種規範相互作用:強相互作用、電磁相互作用和...
STEP(Standard for the Exchange of Product Model Data-產品模型數據互動規範)標準是國際標準化組織制定的描述整個產品生命周期內產品信息的標準,STEP標準是一個正在...
