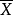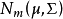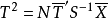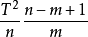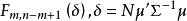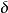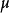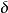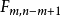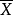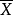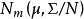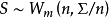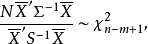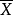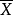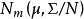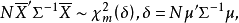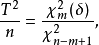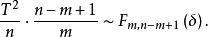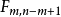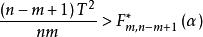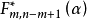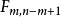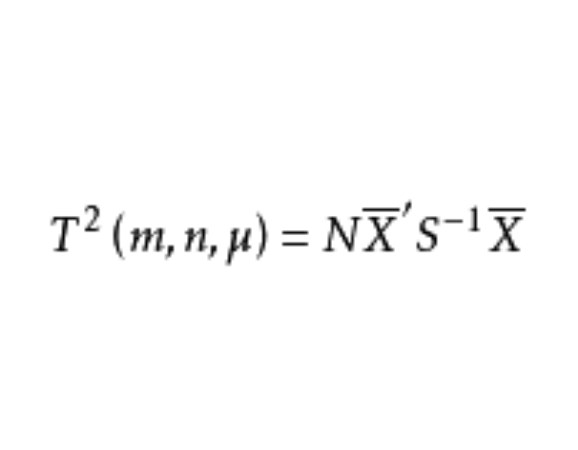設X~Np(μ,∑),S~Wp(n,∑),且X與S相互獨立,n≥p,則稱統計量T2=nX'S-1X的分布為非中心Hotelling T2分布,記為T2~T2(p,n,μ)。當μ=0時,稱T2服從(中心)Hotelling T2分布,記為T2(p,n),由於這一統計量的分布首先由Harold Hotelling提出來的,故稱Hotelling T2分布,值得指出的是,我國著名統計學家許寶碌先生在1983年用不同方法也導出T2分布的密度函式。
基本介紹
- 中文名:霍特林統計量
- 外文名:Hotelling statistic
- 所屬學科:數學(統計學)
- 別名:T2統計量、Hotelling統計量
- 提出者:Harold Hotelling
基本概念
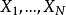
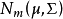
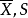
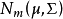
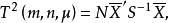
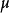
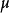
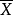
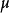
相關結論