各種電漿波反映這種集體性質。在作動力論描述時可以將電漿看成是粒子和波的集合。它們之間存在著相互作用。除了粒子間的相互碰撞外,還有波和粒子相互作用及波和波相互作用。對於它們可以用符拉索夫-麥克斯韋方程組進行研究。
基本信息
詳細內容
線性波和粒子相互作用是波阻尼(或增長)的一個重要機制。一個典型的例子是對符拉索夫-泊松方程作線性微擾分析所得到的電子電漿振盪的線性朗道阻尼。當粒子速度滿足共振條件(其中是波的振盪頻率,是波矢)時受到的波場幾乎不隨時間改變,因此能與波有效地相互作用。如果速度大于波相速的粒子數比速度小于波相速的粒子數要多,那么,總的說來,在波與粒子相互作用時粒子的動能交給波,引起波的增長。在相反情況則引起波的阻尼。因此朗道阻尼與波相速處的粒子分布有關。特別是粒子分布隨速度的變化率的符號決定波到底是阻尼還是增長。束流不穩定性是粒子給波能量使波增長的一例。束流使電漿粒子分布函式在束流速度處有一個附加的峰,使得相速處於粒子速度分布函式的正斜率區域的一些波將會發生不穩定增長。在雷射聚變電漿中經常遇到超熱電子的產生過程,則是由雷射激發的朗繆爾波給粒子能量而自己被阻尼的一例。若線性波和粒子相互作用很小,這時應進一步考慮更高階的非線性波和粒子相互作用,最常見的就是非線性朗道阻尼,其共振條件是即粒子與兩個波的拍波發生相互作用,它可以看成是波在粒子上的散射。
當波在有磁場的電漿中傳播時,粒子除了在波作用下作周期運動外還要在垂直磁場方向上作迴旋運動。當兩者的相位有固定關係時,粒子受到的波場幾乎不變。這時會發生與朗道阻尼相對應的另一種線性波和粒子相互作用──迴旋阻尼。與迴旋阻尼有關的是那些場向速度滿足共振條件-〃〃=的粒子,其中是整數,是粒子的迴旋頻率,〃和〃分別是波矢和粒子速度沿磁場方向的分量。因此迴旋阻尼的值與
處的粒子分布有關。
在波的振幅比較大的時候,不考慮波場對粒子的零級軌道影響的微擾分析不再有效。如果波是一個正弦函式形式的行波,那么總能量處於波谷底部的粒子在以波相速運動的坐標系中近似地作振盪運動,可以認為,當時間達到粒子在波場作用下回彈一次時,應當自洽地考慮波場對粒子的作用,這個時間尺度稱為俘獲時間,(式中是電子質量,是電子電荷,是波數,是波的電場振幅)。因此對於滿足條件(式中呏1/是波振盪時間尺度,=|1/|是波的阻尼或增長的時間尺度)的有限振幅波,俘獲粒子的動力學在問題分析中是重要的。在大振幅電子電漿波的實驗中的確看到當波振幅足夠大時波的阻尼不遵循指數關係,而是發生了振盪,這是與理論分析一致的,表明了俘獲電子與波之間的周期性的能量交換。
如果電漿中存在許多波,而且它們的相位又是無規的,那么可以說電漿處於湍流狀態。目前只是弱湍流才有比較成熟的理論,弱湍流的條件是波能遠小於粒子的熱能,以及波數有一個廣譜。弱湍流理論中最簡單的情形就是只包括線性波和粒子相互作用的準線性理論。這時波譜能量密度的時間變化率通過朗道阻尼機制由粒子的速度平均分布給出。而粒子速度平均分布隨時間變化則遵從一個速度空間的擴散方程,擴散係數與譜能密度有關,因此是一個波與粒子的耦合方程組。平均分布函式的正梯度會引起譜能的增長,而增長的譜能又使平均分布函式擴散,使梯度減小,從而降低了譜能的增長。因此用準線性理論也可解釋一些不穩定性的飽和。弱湍流的條件是十分苛刻的,套用範圍很有限。準線性理論套用得比較成功的一個例子是,低密度束-電漿系統中尾隆不穩定性的飽和問題。
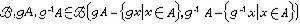 電漿中波和粒子相互作用
電漿中波和粒子相互作用 電漿中波和粒子相互作用
電漿中波和粒子相互作用 電漿中波和粒子相互作用
電漿中波和粒子相互作用 電漿中波和粒子相互作用
電漿中波和粒子相互作用 電漿中波和粒子相互作用
電漿中波和粒子相互作用 電漿中波和粒子相互作用
電漿中波和粒子相互作用 電漿中波和粒子相互作用
電漿中波和粒子相互作用