零一律是安德雷·柯爾莫哥洛夫發現的，也稱柯爾莫哥洛夫零一律，是機率論中的一個定律，指有些事件發生的機率不是幾乎一，就是幾乎零。
基本介紹
- 中文名：零一律
- 外文名：zero-one law
- 定義：有些事件發生機率幾乎一或幾乎零
- 發明人：安德雷·柯爾莫哥洛夫
- 套用領域：機率論
- 套用學科：數學
定義,概述,公式,相關,
定義
在機率理論中，零一律是指出事件必須具有0或1機率且不具有中間值的結果。 有時，聲明是某些機率的極限必須為0或1。
概述
零一律是機率論中的一個定律，它是安德雷·柯爾莫哥洛夫發現的，因此有時也叫柯爾莫哥洛夫零一律。其內容是：有些事件發生的機率不是幾乎一（肯定發生），就是幾乎零（肯定不發生）。這樣的事件被稱為“尾事件”。
尾事件是由無限多的隨機變數的序列來定義的。比如假如我們扔無限多次銀幣，則連續100次數字面向上的事件是一個尾事件。假設
是無限多的獨立的隨機變數（無需同等地分布），則尾事件是一種事件，其發生或不發生由這些隨機變數決定，但不由任何這些隨機變數的有限系列所決定。比如，假如以下系列
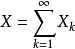收斂，則該事件是一個尾事件。序列和雖收斂但大於1的事件並不是尾事件，因為，比如它不是與X1的值無關。比如假如我們扔無限多次銀幣，則連續100次數字面向上的事件出現無限多次的事件是一個尾事件。無限猴子定理是零一律的一個例子。
公式
柯爾莫哥洛夫零一律更一般的論述是對獨立的 σ-代數流而言的。令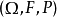
是一個機率空間 和Fn 是包含於 F一列相互獨立的 σ-代數。 令
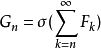是包含
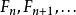的最小的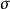
-代數，那么柯爾莫哥洛夫零一律推出對任意的事件
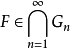，一定有
或1。
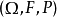
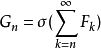
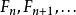
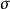
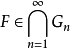
相關
Borel-Cantelli引理，
Blumenthal對馬爾科夫進程的零一律，
恩格爾伯特 - 施密特對於布朗運動的連續，非降級加法函式的零一定律，
休伊特 - 野蠻的零一律可交換序列，
Kolmogorov對於尾部σ代數的零一定律，
Lévy的零一法律，與mart ale會合有關，
拓撲零一律與微型集相關。
