無限猴子定理是來自E.波萊爾一本1909年出版談機率的書籍,當中介紹了“打字的猴子”的概念。
基本介紹
發展簡史
定義
驗證推導
簡要說明
數學證明
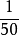
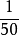

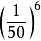
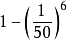
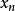

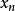
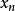
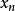
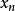
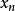

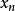
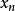
無限長的字元串

機率論證
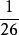


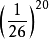
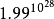
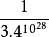


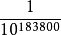

無限猴子定理是來自E.波萊爾一本1909年出版談機率的書籍,當中介紹了“打字的猴子”的概念。
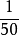
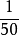

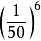
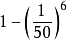

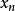
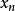
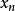

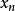
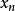

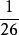


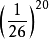
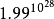
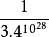


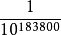
無限猴子定理是來自E.波萊爾一本1909年出版談機率的書籍,當中介紹了“打字的猴子”的概念。...
猴子和打字機(Monkeys and Typewriters),如果無數多的猴子在無數多的打字機上隨機的打字,並持續無限久的時間,那么在某個時候,它們必然會打出莎士比亞的全部著作。...
另一個在流行文化中占了很大分量的思想實驗是“無限猴子定理”,也叫做“猴子和打字機”實驗。定理的內容是,如果無數多的猴子在無數多的打字機上隨機打字,並持續...
無限猴子定理是來自埃米爾·博雷爾一本1909年出版談機率的書籍,當中介紹了“打字的猴子”的概念。這個定理是機率論中的柯爾莫哥洛夫的零一律的其中一個命題的例子...
道德悖論猴子和打字機 另一個在流行文化中占了很大分量的思想實驗是“無限猴子定理”,也叫做“猴子和打字機”實驗。定理的內容是,如果無數多的猴子在無數多的...
編輯 1909年出版了一本書,引起了無限猴子定理這個有趣的 實驗。他在博奕論亦發表過不少論文。1913年和1914年,他的解說論文建立了雙曲幾何和狹義相對論的關係。19...
在道金斯的著作The Blind Watchmaker裡面第三章,他介紹了以下程式, 並且提到了著名的無限猴子定理:I don't know who it was first pointed out that, given ...
比如假如我們扔無限多次銀幣,則連續100次數字面向上的事件出現無限多次的事件是一個尾事件。無限猴子定理是零一律的一個例子。[2] ...
博雷爾集的概念就是以他為名。他1909年出版的一本書,引起了無限猴子定理這個有趣的實驗。他在博弈論亦發表過不少論文。中文名 愛彌兒·波萊爾 國籍 法國 出生...
5. 無限猴子定理/ / 87Chapter 4 學點相對論/ / 891. 狹義相對論/ / 902. 廣義相對論/ / 953. 引力場方程/ / 984. 相對論的實驗驗證和套用/ / ...
一四三、無限猴子定理 211一四四、猴子與進化論 212一四五、通用推薦信 214一四六、蛇與加法器 214一四七、增強版交叉數謎題 216一四八、魔術手帕 216...
無窮或無限,來自於拉丁文的“infinitas”,即“沒有邊界”的意思。其數學符號為...無限猴子定理 無窮公理 銜尾蛇 艾禮富數 無限集合 超現實數 無窮遠焦點...
猴子和打字機(Monkeys and Typewriters)另一個在流行文化中占了很大分量的思想實驗是“無限猴子定理”,也叫做“猴子和打字機”實驗。定理的內容是,如果無數多的...
“……那樣的話乾脆自己一個人,靜靜地煩惱和考慮就好了……那傢伙真是豈有此理,就連思考,也全部丟給身為棋子的貝倫了喔………所謂‘無限猴子定理’,知道嗎?”...
“八百科事典”,來自日文"噓八百"——謊話連篇,法語版名稱的“Désencyclopédie”是根據無限猴子定理而命名,而法語的dé也可解釋作“骰子”,因此法語版的標誌是...
在道金斯的著作The Blind Watchmaker裡面第三章,他介紹了以下程式, 並且提到了著名的無限猴子定理:I don't know who it was first pointed out that, given ...
