雙線性模型(Bilinear model)是介於常規ARMA模型和隨機係數ARMA 模型之間的一種模型。由Granger&Anderson(1978)提出,雙線性模型優點在於保留了ARMA 模型簡單結構的大部分特性。雙線性模型能夠刻畫具有偶然爆發特徵的時間序列,它的另一種常見形式是僅具有AR 結構。
基本介紹
- 中文名:雙線性模型
- 外文名:Bilinear model
- 提出者:Granger&Anderson
- 所屬學科:數學
- 所屬問題:統計學(時間序列分析)
定義
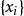

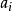



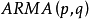
分類







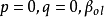





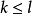

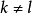



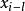

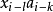
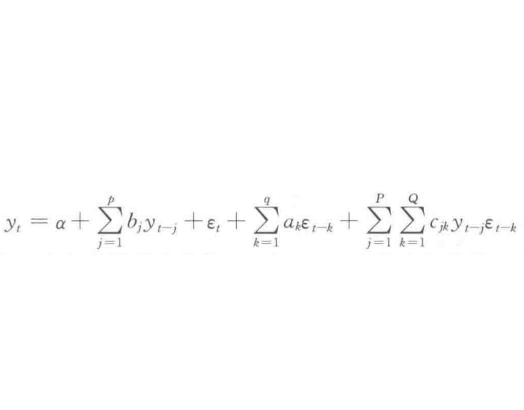
雙線性模型(Bilinear model)是介於常規ARMA模型和隨機係數ARMA 模型之間的一種模型。由Granger&Anderson(1978)提出,雙線性模型優點在於保留了ARMA 模型簡單結構的大部分特性。雙線性模型能夠刻畫具有偶然爆發特徵的時間序列,它的另一種常見形式是僅具有AR 結構。
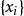

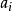



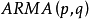







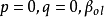





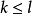

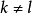



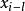

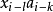
雙線性模型(Bilinear model)是介於常規ARMA模型和隨機係數ARMA 模型之間的一種模型。由Granger&Anderson(1978)提出,雙線性模型優點在於保留了ARMA 模型簡單結構的大...
雙線性系統所屬現代詞,指的是線上性狀態方程(見狀態空間法)中引入狀態變數和控制變數的互動乘積項所導出的一類系統。...
線性系統是一數學模型,是指用線性運運算元組成的系統。相較於非線性系統,線性系統的特性比較簡單。線性系統需滿足線性的特性,若線性系統還滿足非時變性(即系統的輸入...
參數模},忽略系統中一些非主要的影響因素,就主要影響因素建立的模型;將時變參數模型簡化為非時變參數模型;將一般非線性模型簡化為特殊非線性模型,比如雙線性模型等...
在各種特定非線性模型中,以Hammerstein模型和雙線性模型所代表的系統研究得較多.利用這些模型,可以描述眾多的非線性系統,再與一些先進的控制算法相結合以構成非線性...
Clough模型為一種滯回模型。在雙線性模型中,反向載入剛度和初始剛度相同,不能反映混凝土反向載入時損傷積累的影響,這與實際鋼筋混凝土的彎矩--曲率關係有較大差別...
第七章 非線性模型7.1 序言7.2 非參數模型和半參數模型7.3 參數STR模型的設定7.4 STR模型的估計7.5 雙線性模型的設定和估計...
特殊的非線性多變數模型引言4 1非線性自回歸和回歸模型4 2平滑轉換回歸模型4 3雙線性模型4 4非線性移動平均模型4 5異方差和隨機係數模型...
在各種特定非線性模型中,以Hammerstein模型和雙線性模型所代表的系統研究得較多.利用這些模型,可以描述眾多的非線性系統,再與一些先進的控制算法相結合以構成非線性...
給出了詳細的介紹,同時,為了體現參數和非參數方法在時間序列分析中的整合性,還系統地闡述了一些主要參數非線性時間序列模型(比如arch/garch模型和門限模型等)的近期...
非線性時間序列計量經計學的最新進展; 列出許多研究課題的經典專著; 包含參數模型和非參數模型,平穩模型和非平穩模型;參數方法和非參數方法; 增加了對複雜問題所...
反覆殘差法將模型線性化的一種疊代算法,由Subba Rao在處理雙線性模型時提出。 Subba Rao提出了反覆殘差法估算模型參數,該法是在假定模型階數、模型參數初值和計算...
在地震荷載的往復作用下,構件的恢復力與變形的關係曲線在載入和卸載過程中不沿著同一個路徑變化,表現出顯著的滯變特性。常用的結構恢復力的滯變模型有雙線性模型、...
立體參數和疏水參數作為線性回歸分析的變數,隨後,Hansch和日本訪問學者藤田稔夫等人一道改進了Hansch方程的數學模型,引入了指示變數、拋物線模型和雙線性模型等修正,...
立體參數和疏水參數作為線性回歸分析的變數,隨後,hansch和日本訪問學者藤田稔夫等人一道改進了hansch方程的數學模型,引入了指示變數、拋物線模型和雙線性模型等修正,...
第2章混合像元模型6 2.1線性光譜混合模型7 2.2非線性光譜混合模型10 2.2.1Hapke混合光譜模型11 2.2.2Kubelk-Munk混合光譜理論12 2.2.3雙線性模型13 2....
統計學方法,與主成分回歸有關係,但不是尋找回響變數和自變數之間最大方差的超平面,而是通過投影分別將預測變數和觀測變數投影到一個新空間,來尋找一個線性回歸模型...
6. 基於雙線性模型的非線性動態系統最佳化與參數估計集成算法, 控制與決策,1998,Vol.13, No.5 (EI)7. 基於雙線性模型連續非線性動態系統最優控制的DISOPE算法,...
切線模量就是屈服極限和強度極限之間的斜率,用於雙線性彈塑性模型來考慮材料的性能。工程上希望知道其相關模量,從而提出切線模量,是材料非彈性極限範圍內的巨觀的模量...
