雙曲複數

考慮數z = x + jy，其中x,y是實數，j不是實數，j=1

基本介紹

• 中文名：雙曲複數
• 所屬學科：數學

雙曲複數定義

　考慮數z = x + jy，其中x,y是實數，j不是實數，j=1

定義雙曲複數的加法，減法，乘法如下，使之符合交換律、結合律和分配律：

共軛

對於z = x + jy，其共軛值z * = x − jy。對於任何雙曲複數z,w，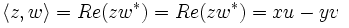

雙曲複數與其共軛雙曲複數同構的證明

(z + w) * = z * + w *

(zw) * = z * w *

(z * ) * = z

可見它是自同構的。

定義內積為 。若 ，說z,w（雙曲）正交。

範數

雙曲複數的範數的平方就取自己和自己的內積，即自身和其共軛值之乘積（閔可夫斯基範數）：

這個範數非正定，其Metric signature是(1,1)。它在乘法下不變。

除法

除了0之外，也不是每個雙曲複數都有乘法逆元。

雙曲複數可逆若且唯若其平方範數非零。

基

雙曲複數有哪些冪等元

列方程。有四個解：1,0,s = (1 − j) / 2,s * = (1 + j) / 2。

s和s^*都是不可逆的。它們可以作雙曲複數的基。z = x + jy = (x − y)s + (x + y)s * 。

若將z = ae + be * 表示成(a,b)，雙曲複數的乘法可表示成(a,b)(c,d) = (ac,bd) 。因此，在這個基里，雙曲複數的加法和乘法和直和R⊕R同構。

共軛可表示為(a,b) * = (b,a)。

幾何

有閔可夫斯基內積的二維實向量空間稱為1+1閔可夫斯基空間，表示為R1,1。正如歐幾理德平面R2的幾何學可以複數表示，閔可夫斯基空間的幾何學可以雙曲複數表示。

在R，對於非零的a，點集 是雙曲線。左邊和右邊的會經過a和 − a。a = 1稱為單位雙曲線。

共軛雙曲線是 ，會分別經過ja和-ja。雙曲線和共軛雙曲線會被成直角的兩條漸近線 分開。

歐拉公式的相應版本是，其中cosh和sinh是雙曲函式

歷史背景

1848年James Cockle提出了Tessarines。1882年威廉·金頓·克利福德以雙曲複數表示自旋和。

20世紀，雙曲複數成為描述狹義相對論的洛侖茲變換的工具，因為不同參考系之間的速度變換可由雙曲旋轉表達。——lp

模長

一個雙曲複數z=a+bj的模為.