一個階梯函式就是一個分段常值函式,只是含有的階段很多但是有限。
基本介紹
- 中文名:階梯函式
- 外文名:staircase function
- 對象:實數函式
- 定義:有限的間隔指標函式的線性組合
- 特點:含有很多階段但是有限
概念


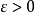







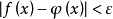

代數性質
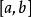

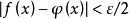

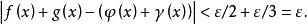















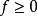







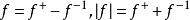



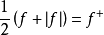

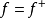



一個階梯函式就是一個分段常值函式,只是含有的階段很多但是有限。


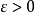







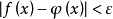

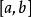

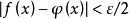

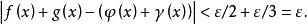















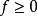







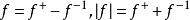



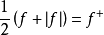

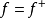


一個階梯函式就是一個分段常值函式,只是含有的階段很多但是有限。...... 一個階梯函式就是一個分段常值函式,只是含有的階段很多但是有限。定義在 上的數值函式 是...
階梯形算法是用於求解雙尺度差分方程的逼近算法,可用於尺度函式和小波函式的構造。...... 階梯形算法是用於求解雙尺度差分方程的逼近算法,可用於尺度函式和小波函式...
分段單調函式是若干個單調函式相接的函式。分段單調函式的定義域可以分成有限個區間,在其中每一個區間上都是單調的一元函式。...
《階梯作業:數學(9年級全1冊)》內容簡介:為了幫助廣大師生更好地理解教科書內容,為教學提供適當的課時作業,我們組織部分一線骨幹教師和教研員編寫了這套《階梯作業...
階梯輸入法是在測定系統入口將作定常態流動的物料從某一時刻起切換為流量與原定常態流動物料相同的含有示蹤劑的流體,同時在系統出口檢測示蹤劑濃度隨時間的變化。...
在數學學科數值分析中,樣條是一種特殊的函式,由多項式分段定義。樣條的英語單詞spline來源於可變形的樣條工具,那是一種在造船和工程製圖時用來畫出光滑形狀的工具...
波萊爾可測函式(Borel measurable function)亦稱波萊爾函式,是與波萊爾集相適應的可測函式。設f(x)是定義在波萊爾集B⊂Rn上的擴充實值函式,若對任意實數α,點集...
數學競賽階梯訓練 出版社 浙江教育出版社 頁數 126頁 ISBN 7533832299 作者 王而冶 許芬英 出版日期 2002年10月1日 開本 16開 第一章 二次函式 第...
一般函式是使用比較普遍的函式,是相對而言的,基礎但很重要。...... 使用比較普遍的函式,但同時它也是構成某整個作用...高斯函式,階梯函式,脈衝函式;在許多程式設計中...
函式的定義:給定一個數集A,假設其中的元素為x。現對A中的元素x施加對應法則f,記作f(x),得到另一數集B。假設B中的元素為y。則y與x之間的等量關係可以用y...
函式y=[x]稱為取整函式,也稱高斯函式。其中不超過實數x的最大整數稱為x的整數部分,記作[x]或INT(x)。該函式被廣泛套用於數論,函式繪圖和計算機領域。...
階梯式廣義預測控制(Stair-like generalized predictive control )多個固定模型可以提高系統的暫態性能,常規自適應模型可以保證系統的穩定性,可重新賦初值的自適應模型...
分布函式(英文Cumulative Distribution Function, 簡稱CDF),是機率統計中重要的函式,正是通過它,可用數學分析的方法來研究隨機變數。分布函式是隨機變數最重要的機率...
《走向清華北大高考階梯訓練(高1數學)》是1998年科學出版社出版的圖書,作者是喬家瑞。...
使用API函式CDdoor來控制光碟機門的開和關程式十分簡單,由於 CDdoor函式自身包含了對異常錯誤的處理機制,因此這個程式的通用性很高,你可以把這段代碼移植到你的程式中...
在一組約束條件下,尋找動力學系統的一組函式,直接函式尋優法是計算機仿真中常用的方法。...
對於服從不連續分布的隨機變數x,x的全體及它們的機率組成的數值表規定了它的分布律。如果用p(x)表示隨機變數從-∞ 到x 的機率,則函式p(x)將是一個單調、非...
若每個神經元的激活函式都是線性函式,那么,任意層數的MLP都可被約簡化成一個等價的單層感知器。 實際上,MLP本身可以使用任何形式的激活函式,譬如階梯函式或邏輯乙...
