對於服從不連續分布的隨機變數x,x的全體及它們的機率組成的數值表規定了它的分布律。
如果用p(x)表示隨機變數從-∞ 到x 的機率,則函式p(x)將是一個單調、非降函式,顯然在 時是零而在x=+∞ 時是1。在一個不連續分布的情況下,它將是一個階梯函式。
基本介紹
定義
分布律
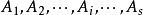






數學期望
偏差
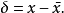


方差

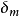

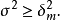
性質
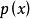


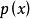
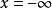


 圖1不連續分布的階梯函式
圖1不連續分布的階梯函式 圖2 連續分布的機率密度函式
圖2 連續分布的機率密度函式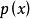
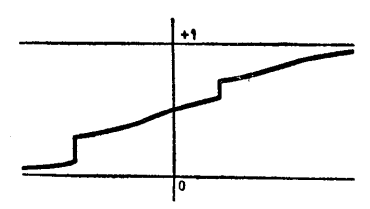 圖3 同時有連續分布與不連續分布
圖3 同時有連續分布與不連續分布對於服從不連續分布的隨機變數x,x的全體及它們的機率組成的數值表規定了它的分布律。
如果用p(x)表示隨機變數從-∞ 到x 的機率,則函式p(x)將是一個單調、非降函式,顯然在 時是零而在x=+∞ 時是1。在一個不連續分布的情況下,它將是一個階梯函式。
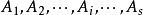






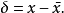



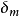

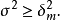
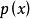


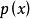
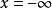


 圖1不連續分布的階梯函式
圖1不連續分布的階梯函式 圖2 連續分布的機率密度函式
圖2 連續分布的機率密度函式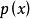
 圖3 同時有連續分布與不連續分布
圖3 同時有連續分布與不連續分布對於服從不連續分布的隨機變數x,x的全體及它們的機率組成的數值表規定了它的分布律。如果用p(x)表示隨機變數從-∞ 到x 的機率,則函式p(x)將是一個單調、非...
總體結構不連續(grossstructural discontinuity)系指幾何形狀或材料的不連續,使結構在較大範圍內的應力或應變發生變化,對結構總的應力分布與變形產生顯著影響。...
間斷分布區又稱不連續分布區。植物的某一分類單位分布在兩個或兩個以上彼此隔離的區域。是植物地理中普遍存在的現象。...
連續分布( continuous distribution)連續型隨機變數X的分布函式是連續的,它對應的分布為連續分布。常用的連續分布有常態分配、均勻分布、指數分布、伽瑪分布、貝塔分布...
連續型分布(continuous distribution)隨機變數的兩個常用的分布類型之一。...... 連續型分布(continuous distribution)隨機變數的兩個常用的分布類型之一。...
連續分布區是指某一植物分類單位(科、屬、種)或群落類型, 其分布區是一塊完整的區域,故名。...
連續機率分布(continuous probability distribution)一個隨機變數在其區間內當能夠取任何數值時所具有的分布。...
按連續與否,分布數列可分為間斷分布數列和連續分布數列兩種 [2] 。1. 間斷分布數列,又稱不連續分布數列。它是只能以整數而不是小數形式出現的分布數列,比如,年齡...
奇異分布是一種機率分布,又稱退化分布,和離散分布、連續分布一起構成機率分布的三種基本類型。奇異分布的典型代表為康托分布。...
一元連續分布一元連續型隨機變數的機率分布。它完全決定於隨機變數的機率密度f(x)。對於數軸R1上的任意(波萊爾)子集A,隨機變數X的值屬於A的機率。 ...
