基本介紹
- 中文名:階乘函式
- 外文名:factorial function
- 領域:數學
定義
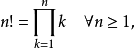
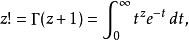
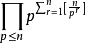
計算
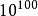
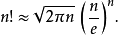
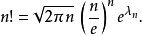
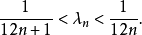
變化
定義擴展
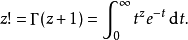
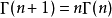
遞進/遞降階乘
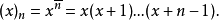
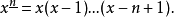
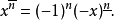
雙階

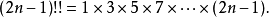
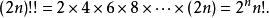
廣義的雙階乘
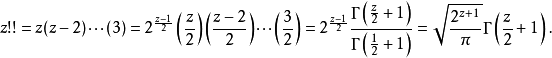
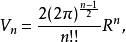
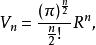
多重階乘
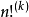
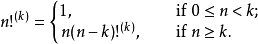
廣義的多重階乘
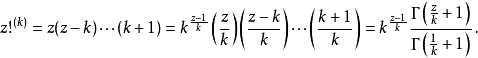
hyper階乘
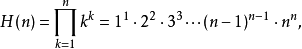
超級階乘
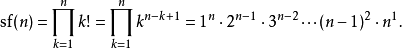
自然數階冪
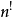
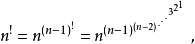
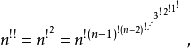
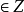
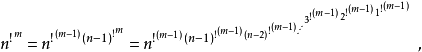

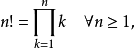
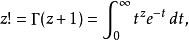
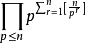
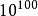
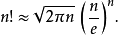
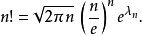
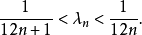
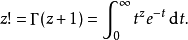
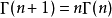
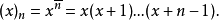
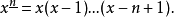
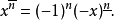

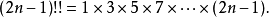
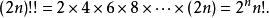
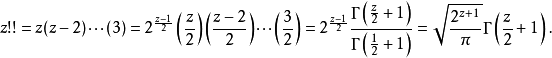
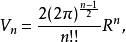
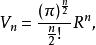
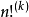
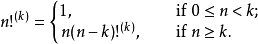
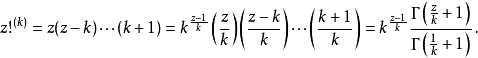
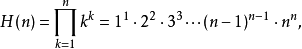
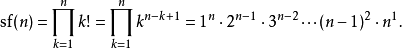
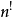
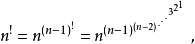
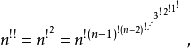
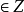
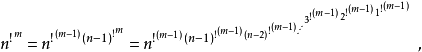
一個正整數的階乘(英語:factorial)是所有小於及等於該數的正整數的積,並且有0的階乘為1。自然數n的階乘寫作n!。1808年,基斯頓·卡曼引進這個表示法。...
階乘是基斯頓·卡曼(Christian Kramp,1760~1826)於 1808 年發明的運算符號,是數學術語。一個正整數的階乘(factorial)是所有小於及等於該數的正整數的積,並且0的...
階乘數定理是由fxccommercial 本人發現並歸納整理的一個新的數學定理猜想,但目前關於這個定理的證明尚無人能給出。...
在數學中,階乘冪是基於連續數列積的一種運算。...... 被用來分別表示上升階乘冪與下降階乘冪。階乘冪上升階乘冪 在特殊函式理論中常用的階乘冪是上升階乘冪用於表達...
伽瑪函式(Gamma函式),也叫歐拉第二積分,是階乘函式在實數與複數上擴展的一類函式。該函式在分析學、機率論、偏微分方程和組合數學中有重要的套用。與之有密切聯繫...
n!中的n為小數或不能寫作整數的分數的階乘稱為廣義階乘。另外,需要注意的是這類階乘不能寫作1×2×…×n。...
嫪麗切拉函式(Lauricella functions)是1893年義大利數學家Giuseppe Lauricella首先研究的三元超幾何函式。...
貝塞爾函式是貝塞爾方程的解,它們和其他函式組合成柱調和函式。除初等函式外,在物理和工程中貝塞爾函式是最常用的函式,它們以19世紀德國天文學家F.W.貝塞爾的姓氏...
巴尼斯G函式是超級階乘函式在複數上的擴展。...... 巴尼斯G函式是超級階乘函式在複數上的擴展。它與Γ函式、K函式以及格萊舍常數(Glaisher constant)有關。巴尼斯G...
安格爾函式是非齊次貝塞爾微分方程的解。貝塞爾函式是貝塞爾方程的解,它們和其他函式組合成柱調和函式。除初等函式外,在物理和工程中貝塞爾函式是最常用的函式,它們以...
Excel是辦公室自動化中非常重要的一款軟體,Excel函式則是Excel中的內置函式。Excel函式共包含11類,分別是資料庫函式、日期與時間函式、工程函式、財務函式、信息函式...
三角函式是數學中屬於初等函式中的超越函式的函式。它們的本質是任何角的集合與一個比值的集合的變數之間的映射。通常的三角函式是在平面直角坐標系中定義的。其定義...
斯特林公式(Stirling's approximation)是一條用來取n的階乘的近似值的數學公式。一般來說,當n很大的時候,n階乘的計算量十分大,所以斯特林公式十分好用,而且,即使在...
與積分相似:連續(或非連續可積)函式的連續和為積分,連續相乘即為積乘。積分表示從一個維度到高一級的維度的轉換,而積乘表示維度的連續變換。...
