階乘冪

在數學中，階乘冪是基於連續數列積的一種運算。

基本介紹

• 中文名：階乘冪
• 外文名：Falling and rising factorials
• 分類：計算機科學

定義

階乘冪通常有兩種形式：上升階乘冪與下降階乘冪。階乘冪有多種書寫方式。由Leo August Pochhammer引進的珀赫哈默爾符號（Pochhammer symbol）是常用的一種。為了區分這兩種階乘冪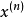， 與 被用來分別表示上升階乘冪與下降階乘冪。

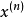
上升階乘冪

在特殊函式理論中常用的階乘冪是上升階乘冪用於表達上升數列的積。上升階乘冪的定義為：

下降階乘冪

在組合數學中（Olver 1999，p.101）也常用下降階乘冪

另外，值得一提的是下降階乘冪實際上是排列 (詳見排列)。

兩者的關係

上升階乘冪與下降階乘冪，兩者之間的關係為：

其中，等號左邊為上升階乘冪，而右邊為下降階乘冪。

階乘冪與階乘的關係為：

其他常用符號

在數學中，階乘冪還有其他的書寫方式。葛立恆(Ronald L. Graham),高德納(Donald E. Knuth) 與 Oren Patashnik 在《具體數學》一書中定義上升階乘冪為：

而他們則定義下降階乘冪為:

另一種常見的上升階乘冪的寫法是:

其中h是遞增公差，而k是數列長度。下降階乘冪則寫作:

一種較為少見的寫法將上升階乘冪 (x)寫作 (x)_(n)

屬性

二項式屬性

零次的上升階乘冪與下降階乘冪，x與 (x)₍₀₎， 都定義為1。 上升階乘冪與下降階乘冪都能以二項式係數形式表達：

於是二項式係數適用的許多性質都適用於階乘冪。

顯然，階乘冪作為n個連續整數的積，它定能被n整除。同時，當n≥4時 階乘冪必定能表達為一個完全平方數減1。

上升階乘冪與下降階乘冪遵從一個類似二項式定理的規則:

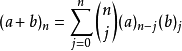
其中待定係數為二項式係數。

顯然 (a)= (a+n− 1)_n

因為下降階乘冪是多項式環的基礎，我們可以將下降階乘冪的積表示為下降階乘冪的線性組合：

等式右邊的係數則為二項式係數。

實數冪

如果 與 都不是負數，階乘冪的指數 可以擴展到實數集合。 運用伽瑪函式，上升階乘冪的定義變為：

下降階乘冪則為:

階乘冪與亞微積分

差分方程里常使用下降階乘冪。其套用與微積分學中的泰勒定理非常相似，不過將微分替換為對應的差分。只是在差分中，下降階乘冪(x)k替代微分中的x. 例如：

與

這種相似性在數學中稱為亞微積分。 亞微積分涵蓋如多項式的二項式型和謝費爾序列.