阿貝爾求和，是一種數學計算方法。
基本介紹
- 中文名：阿貝爾求和
- 所屬學科：數學
阿貝爾求和(Abel summation)級數求和法之一對級數藝a‑，若
阿貝爾求和
則級數藝an,，稱為阿貝爾可和，且S為它的阿貝爾和，記為
阿貝爾求和法是正則的.
阿貝爾求和
相關詞條
- 阿貝爾求和
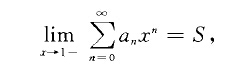
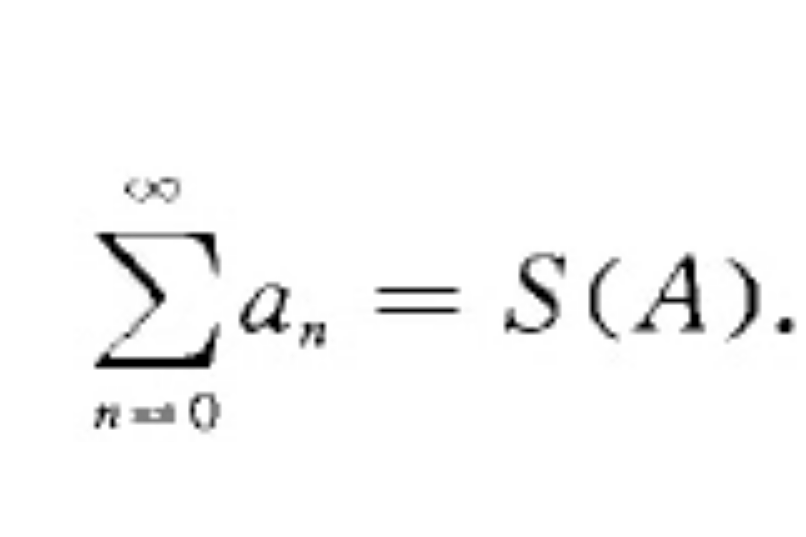
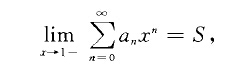
阿貝爾求和，是一種數學計算方法。阿貝爾求和(Abel summation)級數求和法之一對級數藝a‑，若則級數藝an,，稱為阿貝爾可和，且S為它的阿貝爾和，記為阿貝爾求和法是正則的....
- 阿貝爾求和公式
阿貝爾求和公式(Abel's summation formula)亦稱分部求和法.具體內容 阿貝爾求和公式也即阿貝爾變換,若 則 推導過程 套用 是變換分析表達式以進行階的估計所使用的基本方法之一。它有廣泛的套用，對某些問題則可得到相當深刻的結果。
- 數列求和
阿貝爾求和公式 該公式又叫做分部求和公式，是離散型的分部積分法，最早由數學家阿貝爾提出。這個方法也適合解決等差等比數列相乘的數列求和，但比起上面的錯位相減法，該方法方便快捷並且證明十分容易，考試中先寫出證明過程再直接代公式即可...
- 阿貝爾定理
阿貝爾定理的一個有用套用是計算已知收斂級數。方法是通過在級數每項後加上 項，將問題轉換為冪級數求和，最後再計算 x趨於1 時冪級數的極限。由阿貝爾定理可知，這個極限就是原級數的和。1. 為計算收斂級數 ，設 於是有 2. 為計算...
- 阿貝爾積分方程
阿貝爾在數學方面的成就是多方面的。除了五次方程之外，他還研究了更廣的一類代數方程，後人發現這是具有交換的伽羅瓦群的方程。為了紀念他，後人稱交換群為阿貝爾群。阿貝爾還研究過無窮級數，得到了一些判別準則以及關於冪級數求和的定理。
- 阿貝爾函式方程
阿貝爾發現了橢圓函式的加法定理、雙周期性，引進了阿貝爾積分。此外，在交換群、二項級數的嚴格理論、級數求和等方面都有突破性貢獻，但可惜他的論文的價值沒有及時被學術界所認識。施洛德函式方程 施洛德函式方程是一類函式方程。函式方程...
- 自然數冪求和公式
N-1)+(N-2)+...+1的計算公式。其中，所有添加的二項式展開式數，按下列二項式展開式確定，如此可以順利進行自然數的1至n冪的求和公式的遞進推導。（最終推導至李善蘭自然數冪求和公式）二項式定理推導：阿貝爾變換推導：生成函式法：
- 佩龍公式
用阿貝爾求和公式可以得到一個簡單的證明梗概：這不過是在變數代換{\displaystyle x=e^{t}}下的拉普拉斯變換，運用拉普拉斯變換的反轉公式就能得到佩龍公式。例子 由於和狄利克雷級數的關係，佩龍公式常被用於解析數論中的求和。例如我們對...
- 數學危機
他抓住了極限的概念，指出無窮小量和無窮大量都不是固定的量而是變數，並定義了導數和積分；阿貝爾指出要嚴格限制濫用級數展開及求和；狄里克萊給出了函式的現代定義。在這些數學工作的基礎上，維爾斯特拉斯消除了其中不確切的地方，給出現...
- 發散(數學分析術語)
關於發散級數求和的可和法定理 我們說可和法M是正則的，是指它對每個收斂級數求的和，均與其原本柯西意義下的和一致。這類結果被稱為M的阿貝爾型定理，它以阿貝爾定理為原型。更有趣，並且通常也更微妙的是這個結果的部分逆，被稱為...
- 一致收斂判別法
的函式項級數的一致收斂性判別法，它與數項級數一樣，也是基於阿貝爾分部求和公式。定理4（阿貝爾判別法）設 （i）在區間 上一致收斂；（ii）對於每一個 ，是單調一致有界的；（iii）在 上一致有界，即對一切 和正整數n，存在正數M...
- 無字證明 5
一個令人驚訝的“結論”一個等差等比級數 一個交錯幾何級數Ⅱ 阿貝爾變換（阿貝爾求和公式）格線圖中的獨立集與阿茲特克鑽石密鋪 通過完美k叉樹求公比k的等比數列之和 四面體鍵角 彼得松圖的自同構圖與S5同構 文獻索引 ...
- 自由模
（5）自由模的直接求和也是自由的，而自由模的無限笛卡爾乘積通常不是自由的。公式線性組合 給定一個集合E和環R，有一個自由模R，其以E為基礎：即由E索引的R的直接和 顯而易見，它是笛卡爾積的子模組 （R被視為左模組），它由...
