有關結構阻尼矩陣的考慮具有理論與實際重要性(工程結構物大都形式複雜，已考慮用有限元等離散方法模型化，成為多自由度系統)。整體阻尼矩陣（damping matrix）是由質量矩陣和剛度矩陣按比例組合構造而成的。目前工程分析中多採用Rayleigh阻尼陣形式（瑞利阻尼矩陣）即[C]=α[M]+β[K]，其中[M]和[K]分別是系統的質量矩陣和剛度矩陣；α為與質量成比例的係數；β為與剛度成比例的係數。
基本介紹
- 中文名：阻尼矩陣
- 外文名：damping matrix
- 構成：質量矩陣和剛度矩陣按比例組合
- 瑞利阻尼：[C] = α[M] + β[K]
- 參數：α和β為與質量和剛度成比例係數
- 學科：力學
介紹,單元矩陣求取,
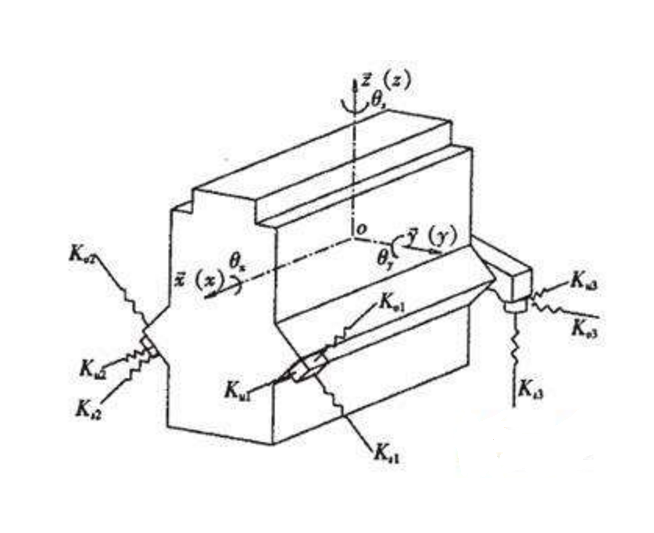
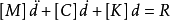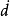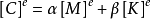介紹
結構的質量矩陣M和剛度矩陣K是由單元質量矩陣m和單元剛度矩Me經過集合而建立起來的。相對來說，阻尼問題比較複雜，結構的阻尼矩陣C不是由單元阻尼矩陣經過集合而得到的，而是根據已有的實測資料，由振動過程中結構整體的能量消耗來決定阻尼矩陣的近似值。可以建立單自由度體系的阻尼矩陣和多自由度體系的阻尼矩陣。
計及阻尼影響的結構動力學方程如下：
式中，[C]為阻尼矩陣；
是隨時間變化的速度矢量。單元阻尼矩陣[C]的表達式為
上式所表達的單元阻尼矩陣是基於和一致質量矩陣同樣的處理方式，因而可稱為一致阻尼矩陣，它假定阻尼力正比於質點的運動速度，這時單元的阻尼矩陣比例於單元質量矩陣。
對於比例於應變速度的阻尼，阻尼力可表示為
，則單元阻尼矩陣為
該單元阻尼矩陣比例於單元剛度矩陣。
由於動力系統的振型對於[M]和[K]是正交的，因此固有振型對比例於[M]和[K]的阻尼矩陣[C]也是正交的，這種阻尼矩陣稱為比例阻尼或振型阻尼矩陣。利用比例阻尼的好處是進行動力問題分析時的各自由度之間可以解耦，從而方便問題的求解。
更一般地，可以將結構的阻尼簡化成[M]和[K]的線性組合，即
其中，α和β是阻尼常數。
單元矩陣求取
相比而言，結構的阻尼問題較為複雜。在地震波傳播過程中，阻尼問題再巨觀上表現為：結構在傳遞地震動能量的同時也消耗了部分能量；在微觀上可理解為材料內部的摩擦耗能和結構內部潛在的接觸面耗能。由於結構波動過程中各種類型的能量耗散機理負責，在一般情況下，實際結構在特定外荷載作用下能夠產生多大的阻尼效應難以事先估計。以下採用瑞利阻尼（Rayleigh Damping）求取單元阻尼矩陣：
式中：α和β為係數，通過選擇合適的α和β係數，可使疊加後得到的阻尼比在較大的頻率範圍內基本保持定值，即與頻率無關，可以基本上反映出岩土體的頻率無關性。α和β可根據下式進行計算：
式中，
為阻尼比，對於岩土體取值範圍為0.02~0.05；ω為中心頻率。
綜上，與三維有限元靜力計算相比，在構造系統運動方程時，動力計算僅需在靜力分析的基礎上求取質量矩陣和阻尼矩陣。同時，根據瑞利阻尼的特點，可不需要專門計算和存儲阻尼矩陣。
