質量沒有加速力,就是說沒有動力聯繫,通過一些矩陣運算,可將這些自由度消去,從而可以減少自由度。這種降低自由度的方法稱為靜力凝聚法。
基本介紹
- 中文名:靜力凝聚法
- 外文名:static condensation method
- 定義:降低自由度的方法
- 套用學科:力學術語
- 範疇:數理科學
- 涉及:質量矩陣
概念,基本原理,
概念
靜力凝聚是結構動力分析中縮減自由度數的一種方法,其基本做法是將結構的自由度分成兩組,一組是反應比較突出的那部分自由度,稱為主自由度,如框架結構樓層的水平位移;另一組為從自由度,如梁端點的豎向位移和轉角。對於低階振型,假設從自由度上慣性力引起的反應部分比較小,可以忽略,其全部反應僅由結構剛度就可以確定。這樣,從自由度向量與主自由度向量之間可以通過剛度矩陣進行轉換,從而使結構的動力方程中只包含主自由度向量,大大減小計算工作量。求出主自由度向量反應後,從自由度反應可以從主、從自由度的關係中求得。
對橋式起重機的質量矩陣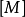 中的元素敬值相差很大,
中的元素敬值相差很大,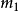 、
、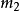 、
、 ,與
,與 、
、 、
、 相差十倍以上。在這種情況下,可以擔這些很小的元素看作零。這樣,這些質量沒有加速力,就是說沒有動力聯繫,通過一些矩陣運算,可將這些自由度消去,從而可以減少自由度。這種降低自由度的方法稱為靜力凝聚法。
相差十倍以上。在這種情況下,可以擔這些很小的元素看作零。這樣,這些質量沒有加速力,就是說沒有動力聯繫,通過一些矩陣運算,可將這些自由度消去,從而可以減少自由度。這種降低自由度的方法稱為靜力凝聚法。
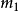
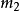




基本原理
靜力凝聚,看似是一個非常深奧的概念,實際上是一個非常簡單的概念。其實我們在國中求解二元一次方程組時就在用靜力凝聚的方法,只是當時沒有提這個概念而已。當時,我們在求解含有x,y兩個未知數的方程組時,可先通過第一個方程,把y用x來表示,然後將此關係式代入第二個方程,從而得到僅包含x一個未知數的全新方程。這個過程其實就是靜力凝聚,它將一個本來含有2個未知數的方程組變為僅含有1個未知數的新方程,在這個過程中,未知數的個數減少了,也就是被“凝聚”了。然後我們從僅包含x一個未知數的新方程求出x的解,再把求出的x代入剛才在凝聚過程中所得到的包含x的y的表達式,從而求出y的解,至此整個方程組得解,求解結束。
以上是靜力凝聚用在求解最簡單的二元一次方程組的基本過程。如果用在一般的矩陣方程組中,靜力凝聚可以這樣理解或表述,先通過矩陣方程組中的部份方程組,使方程中的一部份未知數用其餘的未知數來表達,然後將所得到的未知數關係式代入剩下的方程組,從而求出部份未知數,再代入未知數關係表達式,從而求出剩餘部份未知數的解,即整個方程的全部未知數得解。
在結構工程中,靜力凝聚可以這樣理解或表述,先通過剛度方程中的部份方程組,使方程中的一部份自由度(主自由度)用其餘的自由度(次自由度或從自由度)來表達,然後將所得到的自由度關係式代入剩下的方程組,從而求出一部份自由度(主自由度),再代入自由度關係表達式,從而求出剩餘部份自由度的解,即整個剛度方程的全部自由度得解。
靜力凝聚法中,我們假設阻尼矩陣與質量矩陣的相應項相對應。首先,將儘可能多的質量項化為零,通常只保留樓層平移和轉動的質量項。下面按不同情況分別進行介紹。
(1)質量集中:利用質量集中法建立結構質量分布模型,假設不同自由度的質量相互沒有影響。數十年來,結構工程師都是利用質量集中法模擬結構回響動力的,發表了許多討論不同情況下這種方法的精確性的研究論文。採用質量集中法,質量矩陣即可化為對角矩陣,即如圖1所示:
 圖1
圖1其中,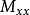 、
、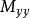 和
和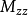 分別表示
分別表示 、
、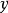 和
和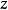 方向的平動相應的質量,
方向的平動相應的質量,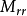 、
、 和
和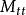 分別表示
分別表示
 、
、 和
和 方向轉動相應的質量,且
方向轉動相應的質量,且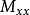 、
、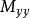 、
、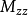 、
、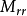 、
、 和
和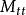 都是對角矩陣。
都是對角矩陣。
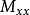
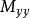
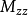

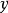
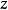
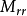

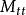



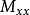
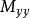
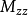
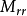

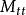
(2)節點轉動慣性矩:與平移質量慣性項相比,節點轉動慣性矩很小,因此對結構的整體回響影響也很小。
(3)垂直質量:節點垂直質量很小,通常假設為零。這種情況下,可以進一步減少系統的自由度。其中,與每個保留的質量項相對的自由度稱為系統的動力自由度。與零質量項對應的自由度可以根據動力自由度計算,所以它們不是獨立變數。因此,與零質量項對應的自由度利用靜力位移關係凝聚,因此,該方法被稱為靜力凝聚法。

