里斯空間是一類有序線性空間。如果半序線性空間E中任何兩個元都有上、下確界,則稱E是里斯空間。
基本介紹
- 中文名:里斯空間
- 外文名:Riesz space
- 套用學科:數學
- 適用領域範圍:有序線性空間
- 適用領域範圍:數理科學
簡介,上下確界,定義,性質,有序線性空間,
簡介
里斯空間是一類有序線性空間。
上下確界
設E是有序線性空間,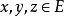 。如果
。如果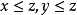 ,則稱z是x和y的一個上界。進而,如果x和y的每個上界u都有
,則稱z是x和y的一個上界。進而,如果x和y的每個上界u都有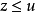 ,則稱z是x和y的最小上界,也稱為上確界或上端,記為sup(x,y)或
,則稱z是x和y的最小上界,也稱為上確界或上端,記為sup(x,y)或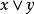 。類似地可以定義x和y的下界,下確界(下端),記為inf(x, y)或
。類似地可以定義x和y的下界,下確界(下端),記為inf(x, y)或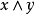 。
。
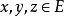
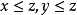
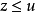
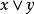
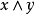
定義
如果半序線性空間E中任何兩個元都有上、下確界,則稱E是里斯空間,此時E對運算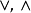 封閉,故也成為格序空間或向量格。
封閉,故也成為格序空間或向量格。
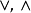
有時也分別稱運算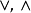 為並和交。記
為並和交。記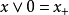 ,
, ,
,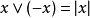 ,分別稱為x的正部,負部和絕對值。滿足
,分別稱為x的正部,負部和絕對值。滿足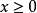 的元稱為正元。
的元稱為正元。
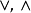
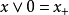

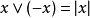
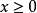
性質
在里斯空間中成立:
1、 ,
,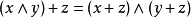 。
。

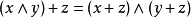
2、 對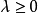 ,有
,有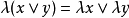 ,
,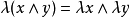 。
。
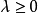
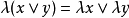
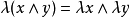
3、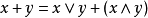 ,特別
,特別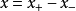 。
。
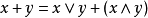
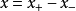
4、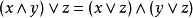 ,
,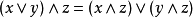 。
。
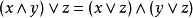
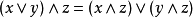
5、 ,
,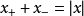 。
。

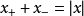
6、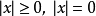 等價於
等價於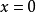 ,
,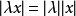 (
(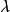 為實數),
為實數),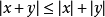 。
。
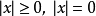
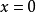
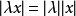
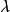
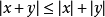
7、 ,
,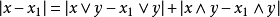 。
。

有序線性空間
設E是實線性空間,並且有序結構,即對E中某些向量對(x,y)有x≥y(或寫作y≤x),“≥”滿足如下條件:對任何x,y,z∈E及實數λ,
1.x≥x;若x≥y且y≥x,則x=y;若x≥y且y≥z,則x≥z。
2.著x≥y,則x+z≥y+z。
3.若x≥y,λ≥0,則λx≥λy,這時稱E是有序線性空間(或稱E是半序線性空間)。
