遞階模糊系統，顧名思義，就是以遞階的形式表示，將幾個低維數模糊系統相連線，從而達到大大減少規則庫內規則數量的問題。遞階模糊系統的結構形式很多，可以是多個低階模糊系統以任何遞階形式相連。可以採用不同的方法隨機生成具有任意輸入變數個數的子模糊系統，構成遞階模糊系統。
基本介紹
- 中文名：遞階模糊系統
- 外文名：Hierarchical fuzzy system
- 分類：計算機 自動化
- 功能：減少規則庫內規則數量
- 結構：多級金字塔
- 相關詞條：模糊系統
簡介,結構形式,結構辨識,構造,
簡介
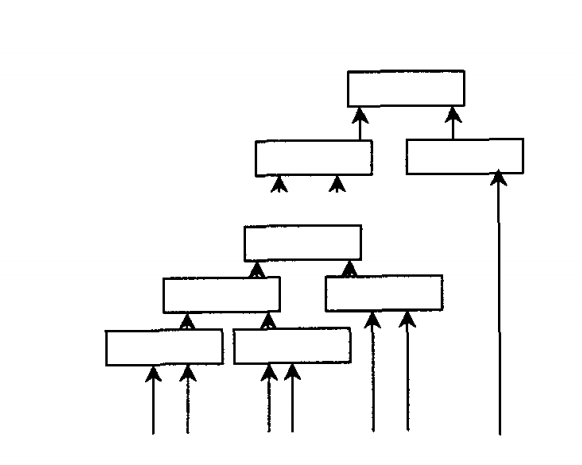
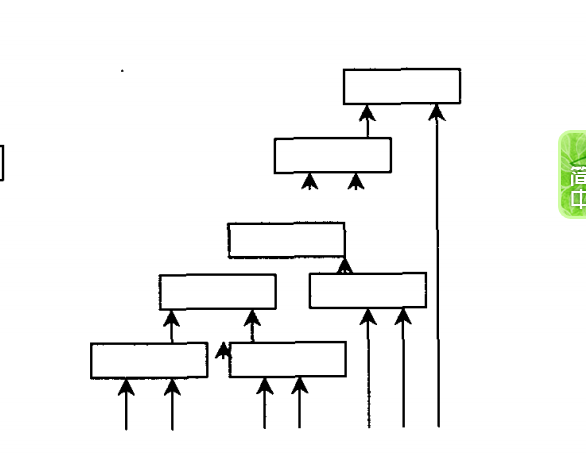
模糊控制領域已經從簡單的系統發展到更複雜系統，隨之而來的問題是：模糊控制器的規則隨著輸入變數數量呈指數增長，在實際套用中要求很大的記憶體，並且難以在實際套用中實現。遞階模糊系統是解決這個“規則爆炸”問題的有效方法，它用遞階的形式將幾個維數很少的模糊系統連線起來，從而達到大大減少規則庫內規則數量的問題。遞階控制的基本原理是把一個總體問題分解成有限數量的子問題。對於複雜的系統，通常採用多級金字塔式的遞階控制結構。
結構形式
遞階模糊系統的結構形式很多，可以是多個低階模糊系統以任何遞階形式相連。可以採用不同的方法隨機生成具有任意輸入變數個數的子模糊系統，構成遞階模糊系統。這是進行遞階模糊系統研究的一個方向。也可以選擇雙輸入二層遞階模糊系統，然後進行結構辨識和參數辨識。我們知道當各級子模糊系統只有兩個輸入時，總規則數目最小。
舉一個遞階模糊系統的典型例子：每個子模糊系統都只有兩個輸入與一個輸出，輸出與另一個輸入變數共同輸入到下一個子模糊系統中，直到最後一個輸入變數。
在這種結構的系統中，若對每個輸入變數
。和中間變數
。進行m個劃分，則總的規則條數為
。對比在傳統通用的模糊系統，其總的規則條數為
，可以看出前者僅是輸入變數個數n的線性函式，而後者卻是n的指數函式，顯然前者要小得多，大大減少了規則數。
結構辨識
遞階模糊系統的結構辨識必須解決每一級子系統輸入變數的配置問題。在實際的問題中，我們知道其中的某些變數比其它變數更重要，對輸出的影響更大。例如變數 通過不同的二維模糊子系統，
只是通過一個模糊子系統；而
，
則通過
個模糊子系統。所以實際的問題是將重要的變數放在或。為了回答這個問題，必須知道輸出是對哪一個變數更敏感。在參數辨識階段，將每一級子系統的希望輸出均設定為最後系統的輸出，然後從第一級開始逐級進行參數的最佳化。應當將最重要的輸入變數配置在第一級，較不重要的放在下一級等等。因此就要對每一個輸入變數的重要性進行排序。
通常我們從要辨識的系統中只能得到許多輸入輸出量，而沒有其它的信息，如何辨識模糊模型的初始結構就變成重要的問題。聚類的目的就是從大量的數據中提取固有的特性，從而獲得系統行為的簡潔表示。它不僅廣泛的套用於數據的組織和分類，而且在數據壓縮和模型構造方面有用處。常見的聚類方法均值聚類、分層聚類、模糊聚類、減法聚類方法等。
構造
在將傳統的模糊系統轉化為一般類型的遞階模糊系統時，除了考慮規則爆炸外，還有就構成遞階模糊系統模糊化，去模糊化所用到的加法器，乘法器，減法器，比較器除法器等)所需要電子元件而言的計算複雜度以及運算時間等問題。
在構造遞階模糊系統時，有時系統輸入變數中的幾個是相關的，通常要將其儘可能地放在同一層。對於具有最小完備規則庫的遞階模糊系統來說，可以選擇另一種結構的系統這兩種特殊結構的遞階模糊系統，如圖1、圖2所示同樣是具有最小完備規則庫的。雖然這兩種系統都是根據最最佳化規則庫原則設計，但在實際套用中使用者要根據情況選擇，並適當修改結構。圖1為輸入變數是偶數，圖2為輸入變數是奇數。
圖1
圖2
